

 |
 |
 |
 |
 |
 |
 |
 |

|

|
- Siano
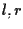 due rette; supponiamo
due rette; supponiamo
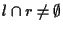 ;
allora
;
allora 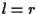 oppure esiste un unico punto
oppure esiste un unico punto 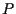 tale che
tale che
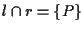 ,
cioè due rette incidenti incidono in un unico punto.
,
cioè due rette incidenti incidono in un unico punto.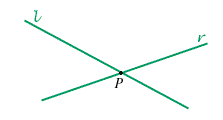
Infatti se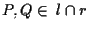 e
e 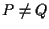 allora
allora 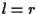 da A1.
da A1.
- In un piano affine esistono almeno due punti distinti; infatti
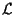 è non vuoto; scelta una retta
è non vuoto; scelta una retta 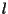 basta poi applicare prima parte di A3.
basta poi applicare prima parte di A3.
- In un piano affine tre punti non allineati sono distinti.
Infatti se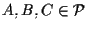 e ad esempio
e ad esempio 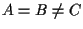 potremo applicare A1 per concludere.
potremo applicare A1 per concludere.
Se invece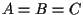 allora esiste un punto
allora esiste un punto 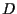 distinto da
distinto da 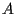 per l'osservazione precedente e ci riconduciamo al caso precedente.
per l'osservazione precedente e ci riconduciamo al caso precedente.
- Esistono almeno tre punti non allineati
Infatti siano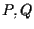 due punti distinti e
due punti distinti e 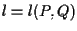 la retta passante per tali punti e sia
la retta passante per tali punti e sia 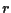 una retta distinta da
una retta distinta da 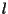 ;
si presentano due casi:
;
si presentano due casi:
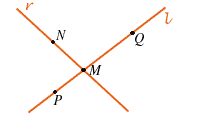
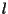 e
e 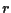 incidenti: posto
incidenti: posto 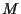 il punto comune a
il punto comune a 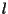 e
e 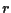 (eventualmente
(eventualmente 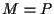 o
o 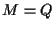 )
sia
)
sia 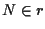 e
e 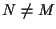 ;
affermiamo che
;
affermiamo che 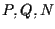 non sono allineati; infatti se una retta contiene
non sono allineati; infatti se una retta contiene 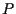 e
e 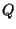 questa è
questa è 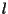 e
e
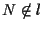 .
.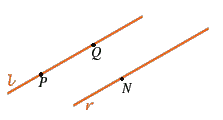
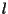 e
e 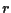 parallele (e quindi disgiunte visto che sono distinte); sia
parallele (e quindi disgiunte visto che sono distinte); sia 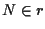 arbitrario; come sopra segue che
arbitrario; come sopra segue che 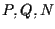 non sono allineati.
non sono allineati.
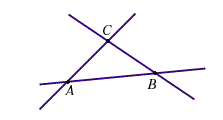
- Esistono almeno tre rette distinte a due a due non parallele.
Infatti se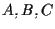 sono tre punti non allineati allora sono distinti; ha senso considerare le rette
sono tre punti non allineati allora sono distinti; ha senso considerare le rette 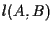 ,
,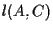 ,
,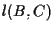 ;
esse sono chiaramente distinte e a due a due incidenti.
;
esse sono chiaramente distinte e a due a due incidenti.
Le osservazioni seguenti sono rivolte a coloro che conoscono i fondamenti della trattazione algebrica degli spazi affini.
Abbiamo dichiarato che le impostazioni algebrica e geometrica di piano affine sono equivalenti, ragion per cui sarebbe lecito aspettarsi che quello che abbiamo definito sopra e chiamato piano affine (che d'ora in poi chiameremo sbrigativamente "piano affine geometrico") soddisfi anche alla definizione algebrica di piano affine (al quale ci riferiremo d'ora in poi come "piano affine algebrico"), cioè in altre parole sia costruibile un spazio vettoriale
Tra l'altro si riconosce immediatamente che il viceversa è vero: in un piano affine algebrico A1, A2 e A3 valgono.
Invece a questo punto non c'è ancora equivalenza tra le due impostazioni nel senso che in generale un piano affine geometrico non è un piano affine algebrico.
Il primo infatti possiede una struttura ancora troppo povera, come si può immaginare esaminando gli assiomi definitori: A1 esprime una proprietà di incidenza, A2 è il V postulato di Euclide e A3 serve per evitare casi banali.
Purtroppo la terminologia tradizionale presenta in questo caso una certa ambiguità, ma ad essa comunque ci atterremo.

 _______________
_______________
 __
__
 ________________________
________________________