ESEMPI: PIANO A 4 PUNTI E PIANO A 9 PUNTI

5. ESEMPIO Sia $\mathcal{P}$ un insieme costituito da 4 elementi distinti $\mathcal{P}=\{A,B,C,D\}$ e $\mathcal{L}$ cosí definito: $\mathcal{L}=\{\{A,B\},\{A,C\},\{A,D\},\{B,C\},\{B,D\},\{C,D\}\}$ .
Affermiamo che $\mathcal{P}$ è un piano affine:

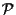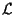A1 vale banalmente visto che ogni sottoinsieme di $\mathcal{P}$ costituito da due elementi sta in $\mathcal{L}$ .
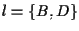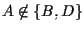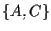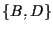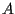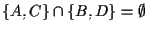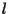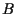A2 si verifica controllando le varie possibilità, ad esempio se $l=\{B,D\}$ e $A \not \in \{B,D\}$ affermiamo che $\{A,C\}$ è l'unica retta parallela a $\{B,D\}$ e passante per : infatti $\{A,C\}\cap\{B,D\}=\emptyset$ , mentre ogni altra retta incide in o .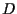
A3 vale in modo evidente.

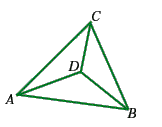
Ponendo $A=(0,0),\;B=(1,0),\;C=(1,1),\;D=(0,1),\;$ $\mathcal{P}$ può venir visto come il piano coordinato su $\mathrm{Z_2}$ .
Diamo ora due possibili rappresentazioni grafiche di tale piano affine: nella prima

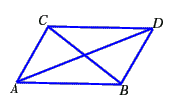due coppie di rette parallele sembrano parallele secondo quello che è il concetto intuitivo di parallelismo della geometria elementare, ma parimenti le rette della terza coppia sembrano proprio intersecarsi e ciò deriva dal fatto che le rette per due punti sono state rappresentate come segmenti della geometria elementare, invece per definizione consistono di due soli punti.
Nella seconda rappresentazione

nessuna delle coppie di rette parallele sembra intersecarsi, ciononostante esse non sembrano rette (o porzioni di rette, cioè segmenti) parallele.
La difficoltà risiede nel fatto che è impossibile ottenere un disegno realistico del piano affine a 4 punti (che non è quello euclideo) su un foglio di carta o sullo schermo (che del piano euclideo sono porzioni).
Poiché il mondo in cui viviamo è localmente euclideo, intendendo con ciò, in parole povere, che la superficie della Terra non è piatta ma comunque si incurva cosí gradualmente che in piccole regioni ci appare tale, molti teoremi della geometria euclidea ci appaiono naturali.

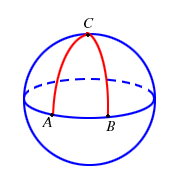D'altra parte teoremi che valgono nel piano euclideo non sono necessariamente veri su altre superfici: per esempio la somma degli angoli di un triangolo nel piano euclideo è $\pi$ laddove nella geometria della sfera un triangolo con un vertice in un polo e due all'equatore ha almeno due angoli retti!
Analoganente nella geometria affine i teoremi della geometria euclidea non sono necessariamente veri per cui non bisogna confidare eccessivamente nell'intuizione geometrica e in particolare, benché sia ancora possibile far riferimento a dei disegni, possiamo fare molto meno affidamento su di essi (rispetto a quanto possibile nella geometria euclidea) per provare teoremi e simili, come discende dagli esempi mostrati.

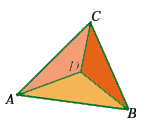
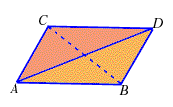
Si noti infine che le due rappresentazioni date possono essere pensate come la stessa (a patto di visualizzarle nello spazio euclideo tridimensionale!) pensando ad un tetraedro osservato da differenti punti di vista.

6. ESEMPIO Sia $\mathcal{P}$ un insieme costituito da 9 elementi distinti $\mathcal{P}=\{A,B,C,D,E,F,G,H,I\}$ e sia $\mathcal{L}$ costituito dai seguenti sottoinsiemi di $\mathcal{P}$ :

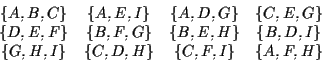
$\begin{displaymath}\begin{array}{cccc} \{A,B,C\} &\{A,E,I\} &\{A,D,G\} &\{C,E,G\... ...\\ \{G,H,I\} &\{C,D,H\} &\{C,F,I\} &\{A,F,H\} \\ \end{array} \end{displaymath}$

Questo è un piano affine: dovrebbe essere verificato che A1,A2 e A3 valgono e questo coinvolge un certo numero di casi: per esempio la retta contenente

è $\{C,F,I\}$ e non ce ne sono altre; anche il secondo assioma si verifica caso per caso; la validità del terzo è ovvia.
Possiamo anche determinare i fasci di rette parallele: esistono 4 fasci distinti costituiti ciascuno da 3 rette che sono state elencate per colonne nella rappresentazione tabulare precedente: ad esempio $\{A,B,C\}\parallel\{D,E,F\}\parallel\{G,H,I\}$ e nessun'altra retta è parallela a queste e cosí via.

Ponendo $A=(0,0),\;B=(1,0),\;C=(2,0),$ $\;D=(0,1),\;E=(1,1),\;F=(2,1),$ $\;G=(0,2),\;H=(1,2),\;I=(2,2),\;$ possiamo pensare al piano affine $\mathcal{P}$ come al piano coordinato su $\mathsf{Z_3}$

______

_______________

________________________