

 |
 |
 |
 |
 |
 |
 |
 |
 |
 |

|

|
Abbiamo dato alcuni esempi di piani affini finiti: il piano affine su
Nel primo esempio avevamo 4 punti, 6 rette, 2 punti su ogni retta e 3 fasci di rette parallele contenenti ciascuno 2 rette; nel secondo esempio avevamo 9 punti, 12 rette, 3 punti su ogni retta e 4 fasci di rette parallele contenenti ciascuno 3 rette; ci chiediamo ora se per ogni intero
La seguente proposizione ci assicura che tutte le rette di un piano affine finito contengono lo stesso numero di punti, anzi in generale due rette di un piano affine hanno la stessa cardinalità:
7. PROPOSIZIONE Sia
DIMOSTRAZIONE Distinguiamo due casi:
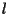 e
e 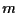 incidenti: allora sappiamo che esiste
incidenti: allora sappiamo che esiste
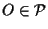 tale che
tale che
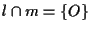 ;
sia
;
sia 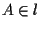 e
e 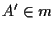 entrambi diversi da da
entrambi diversi da da 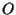 ;
per ogni punto
;
per ogni punto 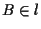 diverso da
diverso da 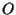 e
e 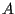 (eventualmente nessuno!) sia
(eventualmente nessuno!) sia 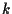 la retta passante per
la retta passante per 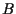 e parallela a
e parallela a 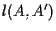 .
.
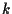 non può essere parallela a
non può essere parallela a 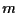 altrimenti avremmo due rette distinte
altrimenti avremmo due rette distinte 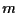 e
e 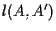 passanti per
passanti per 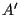 e parallele a
e parallele a 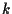 .
Dunque esiste un punto
.
Dunque esiste un punto 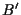 tale che
tale che
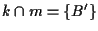 ;
;
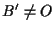 ,
,
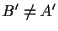 perché altrimenti
perché altrimenti 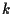 sarebbe incidente a
sarebbe incidente a 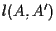 .
.
Definendo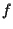 da
da  in
in  ponendo
ponendo 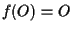 ,
,
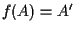 e (eventualmente)
e (eventualmente) 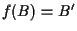 otteniamo la biezione cercata.
otteniamo la biezione cercata.
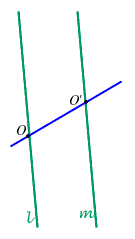
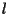 e
e 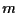 parallele; sia
parallele; sia 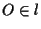 e
e 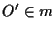 ;
allora
;
allora
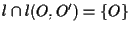 ;
applicando il caso precedente possiamo dire che esiste una corrispondenza biunivoca
;
applicando il caso precedente possiamo dire che esiste una corrispondenza biunivoca 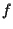 tra
tra 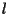 e
e 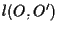 ;
identicamente esiste una biezione
;
identicamente esiste una biezione 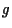 tra
tra 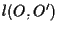 e
e 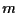 ;
componendo otteniamo che
;
componendo otteniamo che 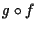 è una corrispondenza tra
è una corrispondenza tra 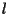 e
e  .
.
8. DEFINIZIONE Sia
9. TEOREMA Sia
-
 contiene esattamente
contiene esattamente 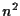 punti
punti
- Ogni punto giace su
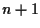 rette
rette
- Ogni fascio di rette parallele contiene
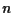 rette
rette
- L'insieme
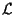 delle rette è costituito da
delle rette è costituito da 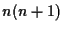 elementi
elementi
- Esistono esattamente
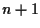 fasci di rette parallele
fasci di rette parallele
DIMOSTRAZIONE
- Supponiamo che
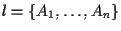 sia una retta in
sia una retta in
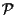 e sia
e sia 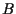 un punto non giacente su
un punto non giacente su 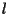 ;
consideriamo la retta
;
consideriamo la retta
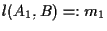 e per ogni
e per ogni
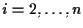 definiamo
definiamo 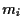 come l'unica retta passante per
come l'unica retta passante per 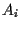 e parallela a
e parallela a 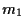 .
.
Ciascuna delle rette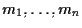 contiene
contiene 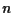 punti e inoltre sono a due a due disgiunte per cui potremo dire che il numero di punti in
punti e inoltre sono a due a due disgiunte per cui potremo dire che il numero di punti in
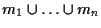 è
è 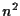 ;
affermiamo che
;
affermiamo che
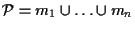 , infatti sia
, infatti sia 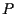 un punto di
un punto di
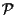 ,
allora
,
allora 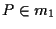 oppure esiste un'unica parallela
oppure esiste un'unica parallela 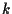 a
a 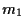 passante per
passante per 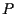 e in questo caso
e in questo caso 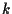 deve incidere
deve incidere 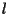 in uno dei punti
in uno dei punti
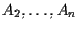 (
(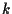 e
e 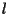 non possono essere parallele perché altrimenti lo sarebbero anche
non possono essere parallele perché altrimenti lo sarebbero anche 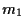 e
e 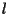 )
e quindi coincidere con una delle rette
)
e quindi coincidere con una delle rette  ,
,

 .
.
- Sia
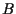 un punto arbitrario di
un punto arbitrario di
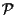 e
e 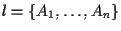 una retta che non lo contiene; definiamo
una retta che non lo contiene; definiamo
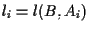 ,
,

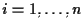 e
e 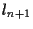 come l'unica retta passante per
come l'unica retta passante per 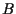 e parallela a
e parallela a 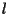 ;
dagli assiomi di spazio affine segue che esse sono
;
dagli assiomi di spazio affine segue che esse sono 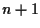 rette distinte per
rette distinte per 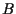 .
.
Inoltre ogni altra retta per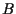 interseca
interseca 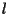 (e dunque è una delle rette
(e dunque è una delle rette 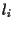 ,
,

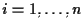 )
oppure è parallela a
)
oppure è parallela a 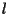 (e dunque è
(e dunque è 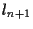 ).
).
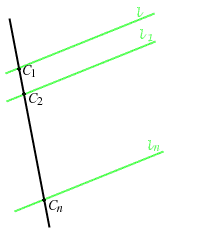
- Sia
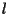 una retta e
una retta e 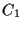 un punto su
un punto su 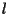 e
e 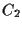 un punto non su
un punto non su 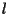 ;
;
possiamo considerare la retta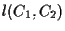 e per ipotesi si potrà scrivere
e per ipotesi si potrà scrivere
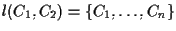 per opportuni punti di
per opportuni punti di
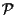 ;
per ogni
;
per ogni
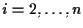 definiamo
definiamo 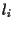 come la retta parallela a
come la retta parallela a 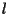 e passante per
e passante per 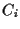 ;
queste
;
queste 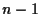 rette sono tutte distinte poiché distinti sono i punti
rette sono tutte distinte poiché distinti sono i punti
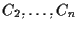 ;
se
;
se 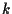 è una retta parallela a
è una retta parallela a 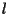 e da questa distinta
allora essa deve intersecare
e da questa distinta
allora essa deve intersecare
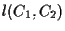 poiché
poiché 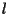 è l'unica parallela a
è l'unica parallela a 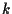 passante per
passante per 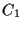 e dunque
e dunque
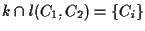 per un qualche
per un qualche 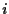 ;
da ciò scende che
;
da ciò scende che 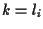 e dunque non esistono altre rette parallele a
e dunque non esistono altre rette parallele a 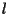 distinte da
distinte da 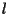 diverse dalle rette
diverse dalle rette 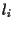 .
.
- Sia
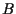 un punto arbitrario di
un punto arbitrario di
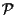 e
e
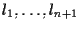 le rette passanti per
le rette passanti per 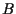 .
Ciascuna di queste rette sta in fascio e i fasci cosí ottenuti sono distinti e contengono ciascuno
.
Ciascuna di queste rette sta in fascio e i fasci cosí ottenuti sono distinti e contengono ciascuno 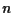 rette cosicché in definitiva abbiamo che l'insieme delle rette per
rette cosicché in definitiva abbiamo che l'insieme delle rette per 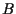 e di tutte le parallele a queste consta di
e di tutte le parallele a queste consta di 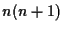 rette; affermiamo che non vi sono altre rette in
rette; affermiamo che non vi sono altre rette in
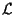 :
infatti se
:
infatti se 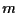 è una retta si ha che
è una retta si ha che 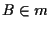 (e in tal caso
(e in tal caso 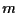 è già stata considerata) oppure esiste una retta contenente
è già stata considerata) oppure esiste una retta contenente 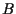 e parallela a
e parallela a 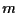 (e anche in questo caso
(e anche in questo caso 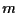 è già stata presa in considerazione).
è già stata presa in considerazione).
- Poiché ciscuna delle
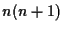 rette sta in un unico fascio e ogni fascio contiene
rette sta in un unico fascio e ogni fascio contiene 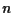 rette, necessariamente si devono avere
rette, necessariamente si devono avere 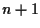 fasci.
fasci.
Osserviamo che da A3 sappiamo che ogni piano affine è di ordine 2 o maggiore e dunque contiene almeno 3 fasci di rette parallele (come già visto direttamente in un punto dell'osservazione 2).
Una domanda naturale che viene naturale porsi è: per quali interi
La risposta è effettivamente sconosciuta e resta uno dei piú grandi problemi aperti in geometria affine finita.
Noi abbiamo visto esempi di piani di ordine 2 e 3; similmente considerando il piano affine coordinato su
In generale se
Invece da tempo è noto che non esistono piani affini di ordine 6, mentre solo recentemente (nel 1989 tramite una ricerca informatica) è stato provato che non esistono piani affini di ordine 10; resta tuttora sconosciuto se esistano o meno piani affini di ordine 12.

 _______________
_______________
 __
__
 ________________________
________________________