TEOREMA DI DESARGUES: INTRODUZIONE

In questa sezione viene introdotto il cosidetto Teorema di Desargues (dal nome del matematico e architetto francese Gérard Desargues (1593-1662) che per primo lo provò).
Il Teorema di Desargues appartiene piú propriamente alla geometria proiettiva e infatti in tale ambito esso afferma che in un piano proiettivo, se abbiamo due triangoli 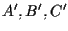e $A,B,C$ (cioè due terne di punti non allineati) senza vertici in comune e consideriamo le rette , e e $r:=A'+B'$ , e , (abbiamo usato la notazione ricorrente in geometria proiettiva per indicare la retta passante per e ) allora le seguenti condizioni sono equivalenti:

$1)\;$ i tre punti $r \cap r'$ , $s\cap s'$ e $t\cap t'$ sono allineati,
$2)\;$ le tre rette , e sono concorrenti.

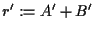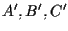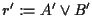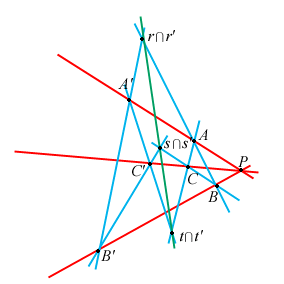
Da questo enunciato di geometria proiettiva si può ricavare l'enunciato affine classico che stabilisce che in un piano affine, se abbiamo due triangoli e $A,B,C$ (cioè due terne di punti non allineati) senza vertici in comune e consideriamo le rette $r:=A\vee B$ , $s:=B\vee C$ e $t:=A\vee C$ e $r:=A'\vee B'$ , $s':=B'\vee C'$ e $t':=A'\vee C'$ , allora si ha che $r\parallel r'$ , $s\parallel s'$ e $t\parallel t'$ implica che le tre rette $A\vee A'$ , $B\vee B'$ e $C\vee C'$ siano parallele o concorrenti.

Orbene: questo teorema non si può ricavare con i nostri assiomi geometrici di piano affine eppure esso vale nel piano ordinario e comunque si può dimostrare nell'ambito della trattazione algebrica in un generico piano affine; già di qui si capisce la necessità di assumere un nuovo assioma che ci permetta di ricavare l'enunciato precedente.
Si potrebbe pensare di assumere come assioma l'enunciato precedente (e sicuramente cosí avremmo risolto i nostri problemi), invece, seguendo l'impostazione data da E. Artin in Geometric Algebra, assumeremo come assioma un'enunciato diverso, al quale ci riferiremo come Teorema di Desargues, e proveremo successivamente l'enunciato classico, che sarà da noi chiamato Teorema di Desargues B.

______

_______________

________________________