TORNA ALLA HOME PAGE TORNA ALL'ELENCO DELLE SEZIONI



precedente
successivo


9. PROPOSIZIONE Il Teorema di Desargues vale in ogni piano affine in cui il Teorema di Desargues B vale.

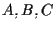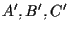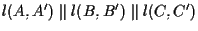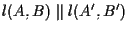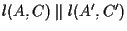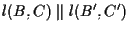DIMOSTRAZIONE di parte I: supponiamo che $A,B,C$ e $A',B',C'$ siano due terne di punti distinti non collineari; e supponiamo che $l(A,A')\parallel l(B,B')\parallel l(C,C')$ e sia $l(A,B)\parallel l(A',B')$ e $l(A,C)\parallel l(A',C')$; dobbiamo dimostrare che $l(B,C)\parallel l(B',C')$.
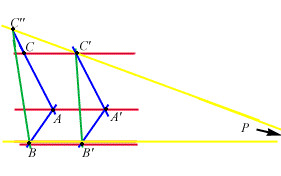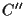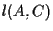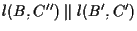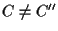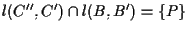Supponiamo per assurdo che ciò non accada e sia $C''$ il punto su $l(A,C)$ tale che $l(B,C'')\parallel l(B',C')$; se $C\neq C''$ allora $l(C'',C')\cap l(B,B')=\{P\}$ per un qualche punto 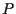$P$ (tali rette non possono essere parallele poiché 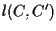$l(C,C')$ è l'unica retta passante per 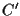$C'$ e parallela a $l(B,B')$).
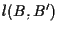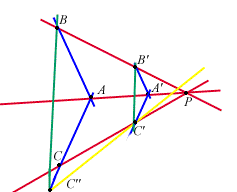
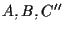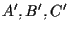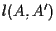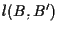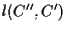Usando il Teorema di Desargues B relativamente alle terne $A,B,C''$ e $A',B',C'$ otteniamo che le rette $l(A,A')$, $l(B,B')$ e $l(C'',C')$ sono parallele o concorrenti, ma le prime due sono parallele e le seconde due incidenti in 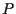$P$, e questo è un assurdo.

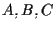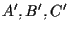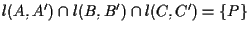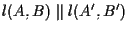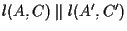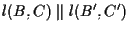Dimostrazione di parte II: supponiamo che $A,B,C$ e $A',B',C'$ siano due terne di punti distinti non collineari; e supponiamo che $l(A,A')\cap l(B,B')\cap l(C,C')=\{P\}$ e sia $l(A,B)\parallel l(A',B')$ e $l(A,C)\parallel l(A',C')$; dobbiamo dimostrare che $l(B,C)\parallel l(B',C')$.
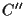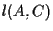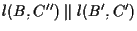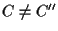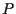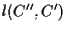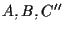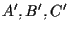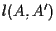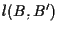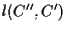Supponiamo per assurdo che ciò non accada e sia come sopra $C''$ il punto su $l(A,C)$ tale che $l(B,C'')\parallel l(B',C')$; se $C\neq C''$ allora $P$ non è contenuto in $l(C'',C')$ ; utilizzando il Teorema di Desargues B relativamente alle terne $A,B,C''$ e $A',B',C'$ otteniamo che le rette $l(A,A')$, $l(B,B')$ e $l(C'',C')$ sono parallele o concorrenti, ma di nuovo le prime due si incontrano in 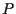$P$ che non giace sulla terza retta.

10. COROLLARIO In ogni piano affine in cui vale il Teorema di Desargues parte II vale anche il Teorema di Desargues.


MAPPA DEL SITO ______ vai in cima alla pagina_______________ precedente__ successivo________________________