TORNA ALLA HOME PAGE TORNA ALL'ELENCO DELLE SEZIONI



precedente
successivo

Enunciamo ora una nuova versione del Teorema di Desargues; per distinguere i due enunciati ci riferiremo sempre a questa nuova versione come "Teorema di Desargues B".
Dimostreremo che in un piano affine $\mathcal{P}$ il Teorema di Desargues è equivalente al Teorema di Desargues B; ciò vuol dire che A1, A2, A3 e A4 implicano il Teorema di Desargues B, ma anche che A1, A2, A3 e il Teorema di Desargues B implicano A4.
In realtà può essere fatto di piú: prima useremo A1, A2, A3 e parte II del Teorema di Desargues per provare il Teorema di Desargues B, poi con A1, A2, A3 e il Teorema di Desargues B proveremo il Teorema di Desargues e in particolare avremo che sarebbe stato sufficiente assumere solo parte II di esso nei nostri assiomi essendo parte I deducibile da A1, A2, A3 e parte II.

8. TEOREMA    TEOREMA DI DESARGUES B
Siano $\mathcal{P}$ piano affine desarguesiano e $A,B,C$,$\;$ $A',B',C'$ due terne di punti non collineari distinti; supponiamo che

\begin{displaymath}l(A,B)\parallel l(A',B'),\;\; l(A,C)\parallel l(A',C'),\;\;l(B,C)\parallel l(B',C'). \end{displaymath}

Allora le rette $l(A,A'),\;l(B,B'),\;l(C,C')$ sono parallele o concorrenti:

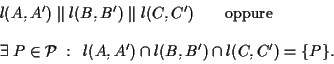
\begin{displaymath}\begin{array}{l} l(A,A')\parallel l(B,B')\parallel l(C,C')\;\... ...hcal{P}\;:\;\;l(A,A')\cap l(B,B')\cap l(C,C')=\{P\}.\end{array}\end{displaymath}

DIMOSTRAZIONE 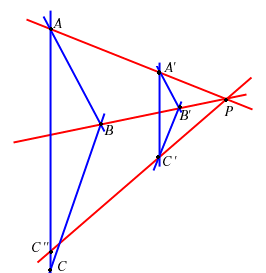Se le rette $l(A,A'),\;l(B,B')$ e $\;l(C,C')$ non sono parallele allora due di esse devono incidere in un qualche punto $P$; supponiamo ad esempio che $l(A,A')\cap l(B,B')=\{P\}$ e poniamo $l(C',P)\cap l(A,C)=\{C''\}$ (queste ultime due rette non possono essere parallele e disgiunte; se coincidenti invece e saremmo ugualmente a posto).
Usando parte II del Teorema di Desargues relativamente alle terne 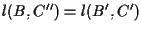$A,B,C''$,$\;$ $A',B',C'$ otteniamo che $l(B,C'')\parallel l(B,C')$; ma $l(B,C)$ è l'unica retta passante per $B$ e parallela a $l(B',C')$ e quindi $l(B,C)=l(B,C'')$; ma questa retta interseca $l(A,C)$ in alpiú un punto e dunque $C=C''$ e $P\in l(C,C')$.

Si noti quindi che nella dimostrazione si è utilizzato solamente parte II del Teorema di Desargues.
MAPPA DEL SITO ______ vai in cima alla pagina_______________ precedente__ successivo________________________