INDIPENDENZA DEL TEOREMA DI DESARGUES DAGLI ASSIOMI DI PIANO AFFINE

L'enunciato dell'assioma A4 è un teorema in altri diversi e piú usuali contesti (ad esempio nell'ambito della geometria formalizzata dagli assiomi di Hilbert oppure nell'ambito della teoria degli spazi affini algebrici).

Ora invece esso non può essere dedotto dagli assiomi A1, A2 e A3 di piano affine e pertanto deve venir assunto come assioma se vogliamo lavorare in ambiente in cui poter affermare la sua validità.

Il fatto che A4 sia indipendente da A1, A2 e A3 non è affatto banale (ciò tra l'altro ridimostra che un piano affine geometrico non è un piano affine algebrico); il controesempio piú semplice è costituito dal cosiddetto piano di Moulton a cui brevemente accenneremo:

2. CONTROESEMPIO IL PIANO DI MOULTON
Il piano di Moulton è un piano affine in cui il teorema di Desargues non vale e, come suggerito dal nome, esso fu esibito dall'astronomo statunitense F.R. Moulton (1872-1952) nel 1902 nell'articolo "A simple non-Desarguesian plane Geometry" in Trans. Amer. Math. Soc. vol. 3 pp. 192-195 .
L'insieme dei punti $\mathcal{P}$ è $\mathbf{R}^2$ e l'insieme $\mathcal{L}$ delle rette di $\mathcal{P}$ è cosí definito: $\mathcal{L}$ consiste di tutte le rette euclidee (della geometria analitica) verticali e orizzontali o con pendenza negativa, cioè con equazione e $m\ < 0$ e inoltre dalle "rette spezzate" costituite da rette euclidee (della geometria analitica) con pendenza positiva sopra l'asse e al di sotto dello stesso, cioè: $\{(x,y)\in\mathbf{R}^2\;:\;\;y=mx+q,\;x\geq 0\}\cup\{(x,y)\in\mathbf{R}^2\;:\;\;y=2mx+q,\;x< 0\}$ ove e $q\in\mathbf{R}$ .
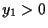È un esercizio di geometria analitica mostrare che ogni coppia di punti distinti , giace su un unica retta del piano di Moulton: l'unico caso che presenta una minima difficoltà si presenta quando un punto ha orinata positiva e l'altro negativa e la retta euclidea per questi due punti ha invece pendenza positiva; in tal caso si può procedere scrivendo i fasci di rette per e rispettivamente in questo modo (qui supponiamo e )

$\begin{displaymath}\begin{array}{l} (y-y_1)=m(x-x_1)\\ (y-y_2)=2m(x-x_2) \end{array} \end{displaymath}$

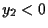e imponendo che il punto di intersezione con l'asse

sia lo stesso:

$\begin{displaymath}\frac{-y_1+mx_1}{m}=\frac{-y_2+2mx_2}{2m}\end{displaymath}$

Da questa equazione in

otteniamo

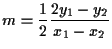e in definitiva abbiamo che A1 vale.
Per quel che riguarda il parallelismo, si ha che rette orizzontali sono parallele cosí come rette verticali ed ancora rette con medesima pendenza negativa; per quel che riguarda le "rette spezzate" esse sono parallele se e solo se hanno medesima pendenza al di sopra e al di sotto dell'asse

e di qui si vede facilmente che vale A2.
L'assioma A3 chiaramente vale.
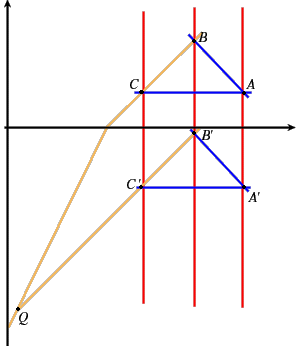
A questo punto la maniera più semplice per verificare che nel piano di Moulton il Teorema di Desargues non vale è osservare la figura seguente in cui le ipotesi del Teorema di Desargues sono verificate ma $l(B,C)\cap l(B',C')=\{Q\}$ .

______

_______________

________________________