IL TEOREMA DI DESARGUES: ENUNCIATO

TORNA ALLA HOME PAGE

TORNA ALL'ELENCO DELLE SEZIONI

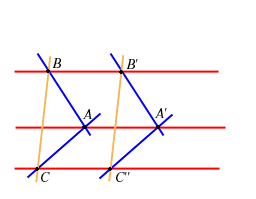
Arricchiamo ora la struttura di piano affine assumendo un altro assioma: precisamente assumiamo che valga il Teorema di Desargues:

1. DEFINIZIONE

A4 Sia un piano affine e siano e 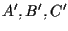due terne di punti distinti, non collineari; $\mathcal{P}$ è detto piano affine desarguesiano se vale il seguente assioma, detto Teorema di Desargues:

I
Supponiamo che le rette e siano parallele: ;
se e allora .

II
Supponiamo che le rette e siano concorrenti, cioè $\exists\;P\in\mathcal{P}$ tale che $l(A,A')\cap l(B,B') \cap l(C,C')=\{P\}$ ;
se $l(A,B)\parallel l(A',B')$ e $l(A,C)\parallel l(A',C')$ allora $l(B,C)\parallel l(B',C')$ .

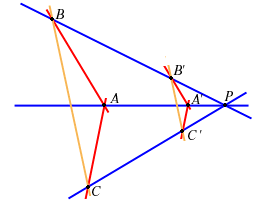
Un piano affine in cui A4 vale è detto desarguesiano.

Dicendo che

e

sono due terne di punti distinti, non collineari intendiamo che i sei punti

sono distinti, che

non sono collineari e

non sono collineari; per definizione una terna di punti non collineari costituisce i vertici di un triangolo e dunque possiamo riformulare l'ipotesi precedente del Teorema di Desargues dicendo che

e

costituscono i vertici di due triangoli senza vertici in comune.

MAPPA DEL SITO

______

vai in cima alla pagina

_______________

precedente

__

successivo

________________________