|
|
Sia
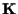 un campo; vogliamo provare che
un campo; vogliamo provare che
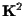 è desarguesiano.
è desarguesiano.
Premettiamo una definizione e alcuni lemmi:
3. DEFINIZIONE
Sia
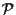 un piano affine; siano
un piano affine; siano 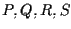 4 punti distinti e non collineari di
4 punti distinti e non collineari di
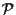 ;
si dice che ;
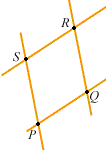
si dice che 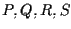 costituiscono i vertici di un parallelogramma se
costituiscono i vertici di un parallelogramma se
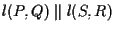 e
e
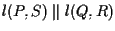 . .
D'ora in poi lavoreremo in
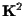 e useremo la sua naturale struttura di
e useremo la sua naturale struttura di
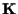 -spazio vettoriale: porremo -spazio vettoriale: porremo
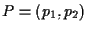 , ,
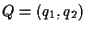 , ,
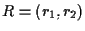 , ,
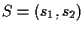 e scrivere, ad esempio,
e scrivere, ad esempio, 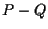 significherà
significherà
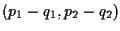 e parimenti, se
e parimenti, se
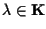 , ,
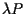 vorrà dire
vorrà dire
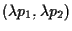 ;
si noti ancora che supporre che la retta ;
si noti ancora che supporre che la retta 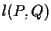 non sia né verticale né orizzontale significa
non sia né verticale né orizzontale significa
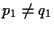 e
e
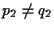 . .
4. LEMMA
Siano 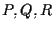 tre punti distinti di
tre punti distinti di
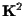 ;
allora ;
allora 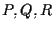 sono collineari se e solo se esiste
sono collineari se e solo se esiste
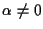 tale che
tale che
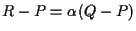 . .
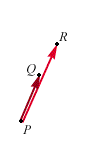
DIMOSTRAZIONE
Supponiamo per semplicità che la retta per 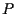 e
e 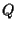 non sia verticale o orizzontale; allora essa avrà un'equazione:
non sia verticale o orizzontale; allora essa avrà un'equazione:
-il secondo membro esiste ed è non nullo nelle nostre ipotesi- e quindi
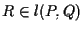 se e solo se
se e solo se
che possiamo anche scrivere
da cui segue
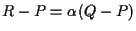 ;
similmente si tratta il caso in cui ;
similmente si tratta il caso in cui 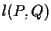 è orizzontale o verticale.
è orizzontale o verticale.
5. LEMMA
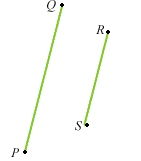
Siano 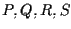 4 punti distinti di
4 punti distinti di
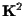 ;
allora ;
allora
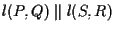 se e solo se esiste uno scalare non nullo
se e solo se esiste uno scalare non nullo 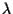 tale che
tale che
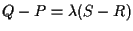 . .
 DIMOSTRAZIONE
Ancora per semplicità supponiamo di non aver a che fare con rette orizzontali o verticali.
DIMOSTRAZIONE
Ancora per semplicità supponiamo di non aver a che fare con rette orizzontali o verticali.
La retta 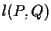 ha pendenza
ha pendenza
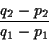
e la retta 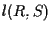 ha pendenza
ha pendenza
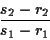 .
.
Abbiamo quindi che
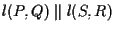 se e solo se
se e solo se
(è noto dalla geometria analitica che in
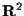 due rette sono parallele se e solo se sono verticali oppure hanno la stessa pendenza; identicamente in
due rette sono parallele se e solo se sono verticali oppure hanno la stessa pendenza; identicamente in
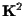 )
uguaglianza che possiamo pure riscrivere come )
uguaglianza che possiamo pure riscrivere come
ove
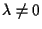 ;
e di qui segue che ;
e di qui segue che
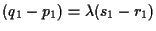 e
e
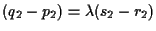 .
In maniera analoga si trattano i casi in cui .
In maniera analoga si trattano i casi in cui 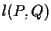 e
e 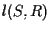 sono verticali o orizzontali.
sono verticali o orizzontali.
6. LEMMA
Siano 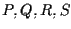 4 punti distinti e non collineari di
4 punti distinti e non collineari di
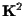 ;
proviamo che ;
proviamo che 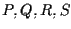 costituiscono i vertici di un parallelogramma se e solo se
costituiscono i vertici di un parallelogramma se e solo se 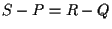 . .
DIMOSTRAZIONE
Supponiamo che 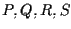 costituiscano i vertici di un parallelogramma, allora da lemma 5 sappiamo che esistono
costituiscano i vertici di un parallelogramma, allora da lemma 5 sappiamo che esistono
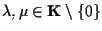 tali che
tali che
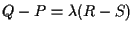 e
e
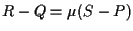 . .
Se 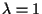 (equivalentemente
(equivalentemente 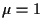 )
siamo a posto; altrimenti, se per assurdo )
siamo a posto; altrimenti, se per assurdo
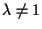 (e quindi
(e quindi 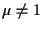 ),
partendo dall'identità ),
partendo dall'identità
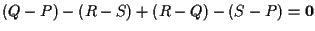 potremo scrivere
potremo scrivere
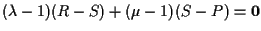 cioè
cioè
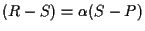 con
con
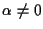 ,
quindi per lemma 4 ,
quindi per lemma 4 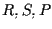 sono allineati e siccome
sono allineati e siccome
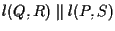 dal postulato delle parallele segue che
dal postulato delle parallele segue che
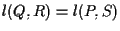 e quindi
e quindi 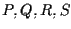 allineati contro l'ipotesi; similmente nei casi in cui abbiamo rette verticali o orizzontali.
allineati contro l'ipotesi; similmente nei casi in cui abbiamo rette verticali o orizzontali.
Viceversa se 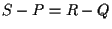 concludiamo da lemma 2 che
concludiamo da lemma 2 che
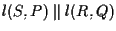 ;
ma anche possiamo scrivere ;
ma anche possiamo scrivere 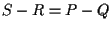 e quindi concludere che
e quindi concludere che
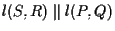 . .
7. PROPOSIZIONE
Il piano affine
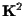 è desarguesiano.
è desarguesiano.
DIMOSTRAZIONE
Proviamo che vale parte I di A4: siamo quindi 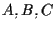 , ,
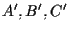 due terne di punti distinti, non collineari;
due terne di punti distinti, non collineari;
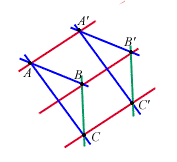 e sia
e sia
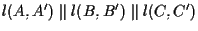 ; ;
supponiamo che
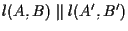 e
e
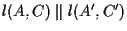 :
vogliamo provare che :
vogliamo provare che
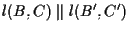 . .
Notiamo che 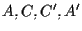 sono i vertici di un parallelogramma e quindi
sono i vertici di un parallelogramma e quindi 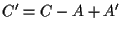 ed anche
ed anche 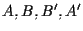 sono i vertici di un parallelogramma da cui
sono i vertici di un parallelogramma da cui 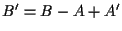 ;
quindi ;
quindi 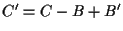 e dunque anche
e dunque anche 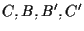 costituiscono i vertici di un parallelogramma per cui
costituiscono i vertici di un parallelogramma per cui
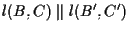 . .
Proviamo che vale parte II di A4:
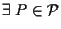 tale che
tale che
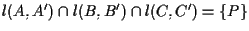 ; ;
se
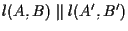 e
e
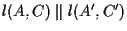
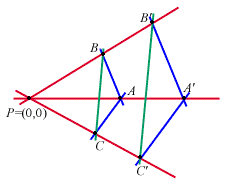 vogliamo provare che
vogliamo provare che
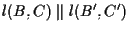 ;
supponiamo senza ledere la generalità che ;
supponiamo senza ledere la generalità che 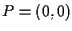 e quindi da lemma 4 segue che esistono
e quindi da lemma 4 segue che esistono
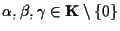 tali che
tali che
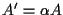 , ,
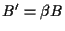 , ,
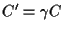
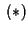 ;
se dimostreremo che ;
se dimostreremo che
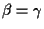 potremo concludere che
potremo concludere che
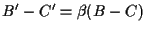 e dunque che
e dunque che
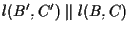 da lemma 5. da lemma 5.
Per ipotesi
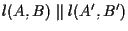 e
e
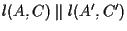 ,
condizione che possiamo riscrivere in termini di pendenza (sempre supponendo di non avere a che fare, per semplicità, con rette verticali o orizzontali) come ,
condizione che possiamo riscrivere in termini di pendenza (sempre supponendo di non avere a che fare, per semplicità, con rette verticali o orizzontali) come
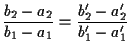 e
e
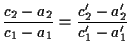
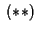 ove come al solito si è posto
ove come al solito si è posto
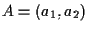 e cosí via; con questa notazione le equazioni
e cosí via; con questa notazione le equazioni 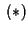 si possono riscrivere come
si possono riscrivere come
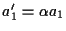 , ,
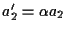 , ,
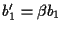 , ,
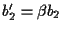 e
e
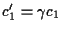 , ,
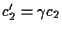 che immesse nella prima delle equazioni
che immesse nella prima delle equazioni
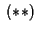 danno danno
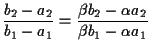 , cosa
che implica, basta fare qualche calcolo, , cosa
che implica, basta fare qualche calcolo,
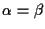 (si ricordi che (si ricordi che 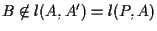 ). ).
Identicamente dalla seconda delle
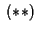 otteniamo
otteniamo
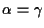 e in definitiva la nostra tesi.
e in definitiva la nostra tesi.
Dovrebbe esser chiaro intuitivamente che se
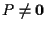 allora potremo sempre ricondurci al caso precedente
sottraendo
allora potremo sempre ricondurci al caso precedente
sottraendo 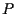 da
da
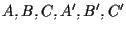 e ottenendo in tal modo una configurazione che soddisfa, si vede facilmente, l'ipotesi del caso precedente.
e ottenendo in tal modo una configurazione che soddisfa, si vede facilmente, l'ipotesi del caso precedente.
|















![]() tre punti distinti di
tre punti distinti di
![]() ;
allora
;
allora ![]() sono collineari se e solo se esiste
sono collineari se e solo se esiste
![]() tale che
tale che
![]() .
.

![]() e
e ![]() non sia verticale o orizzontale; allora essa avrà un'equazione:
non sia verticale o orizzontale; allora essa avrà un'equazione: 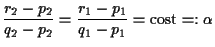
![]() 4 punti distinti di
4 punti distinti di
![]() ;
allora
;
allora
![]() se e solo se esiste uno scalare non nullo
se e solo se esiste uno scalare non nullo ![]() tale che
tale che
![]() .
.
 DIMOSTRAZIONE
Ancora per semplicità supponiamo di non aver a che fare con rette orizzontali o verticali.
DIMOSTRAZIONE
Ancora per semplicità supponiamo di non aver a che fare con rette orizzontali o verticali.
![]() ha pendenza
ha pendenza
![]()
![]() ha pendenza
ha pendenza
![]() .
.![]() se e solo se
se e solo se  e sia
e sia
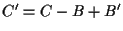 e dunque anche
e dunque anche  vogliamo provare che
vogliamo provare che
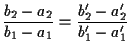 e
e
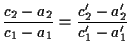
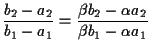 , cosa
che implica, basta fare qualche calcolo,
, cosa
che implica, basta fare qualche calcolo,
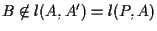 ).
).

 _______________
_______________
 __
__
 ________________________
________________________