TEOREMA DI PAPPO

Mostreremo ora la caratterizzazione geometrica della commutatività della moltiplicazione:

9. TEOREMA TEOREMA DI PAPPO
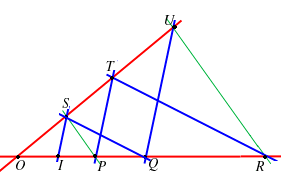
Sia $\mathcal{P}$ un piano affine desarguesiano e due rette in $\mathcal{P}$ incidenti in un punto ; siano $P,Q,R\in l$ e $S,T,U \in m$ punti distinti da . Se $l(P,T)\parallel l(Q,U)$ e $l(Q,S)\parallel l(R,T)$ allora $l(P,S)\parallel l(R,U)$ .

Questa affermazione può essere vera o falsa in un generico piano affine desarguesiano come chiarito dalla seguente proposizione e dall'osservazione precedente:

10. PROPOSIZIONE Sia $\mathcal{P}$ un piano affine desarguesiano; allora il Teorema di Pappo è vero se e solo se la moltiplicazione fra punti delle sue rette è commutativa.

DIMOSTRAZIONE Siano rette e punti come nel Teorema di Pappo (configurazione di Pappo); e sia $I\in l$ tale che $l(I,S)\parallel l(P,T)$ ; consideriamo la moltiplicazione di punti su relativamente ad e : moltiplicando e usando (e ) otteniamo $P\cdot Q =R$ .
A questo punto se il teorema di Pappo è vero otteniamo che anche $Q\cdot P=R$ (basta moltiplicarli usando -e -) e dunque la moltiplicazione è commutativa (per ogni retta e per ogni coppia di punti distinti su possiamo trovare una configurazione di Pappo come sopra).
Viceversa se il Teorema di Pappo è falso allora si ha che $P\cdot Q =R$ ma $Q\cdot P\neq R$ , cosicché la moltiplicazione di punti su relativamente ad e non è commutativa.

Un piano affine in cui vale il Teorema di Pappo è detto pappiano; poiché si può mostrare che il Teorema di Pappo implica il Teorema di Desargues (si veda G. HESSEMBERG, "Beweis des Desarguesschen Satzes aus dem Pascalschen" in Math. Ann., 61, (1905), pp. 161-172), e dunque un piano affine pappiano è desarguesiano.
Per quanto detto sopra invece non vale il viceversa, tuttavia esso vale per piani desarguesiani finiti e questa asserzione è equivalente all'importante teorema di algebra (Teorema di Wedderburn) che afferma che ogni corpo finito è un campo.

______

_______________

________________________