TORNA ALLA HOME PAGE TORNA ALL'ELENCO DELLE SEZIONI




precedente
successivo

Nella sezione precedente abbiamo definito un'operazione tra i punti di una retta retta affine $l$ relativamente alla scelta di un fissato punto $O$ su $l$; abbiamo visto che $(l,+)$ è un gruppo commutativo (si noti che dipende da $O$); vogliamo ora definire un'altra operazione interna su $l$, la moltiplicazione fra punti, in modo da ottenere $(l,+,\cdot)$ campo.
A tal fine però la struttura di piano affine desarguesiano è troppo povera, e ci permetterà solamente di ottenere un corpo, come vedremo in dettaglio.
Sarà necessario richiedere un altro assioma per poter ottenere un campo.

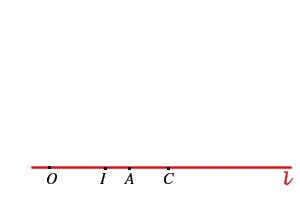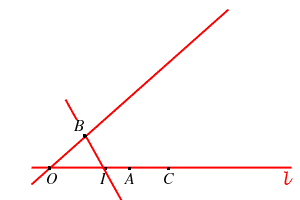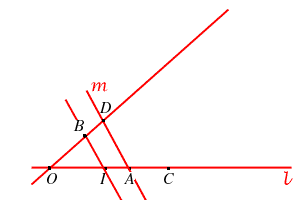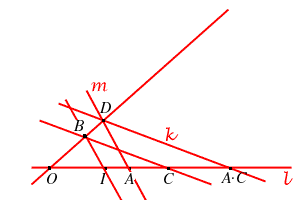
4. DEFINIZIONE MOLTIPLICAZIONE SULLE RETTE DI UN PIANO AFFINE DESARGUESANO
 Sia $\mathcal{P}$ un piano affine desarguesiano e $l\in \mathcal{L}$ una retta in $\mathcal{P}$; siano $O,I\in l$ due punti distinti e siano $A,C\in l$.
Definiamo il punto $A\cdot C$ (detto prodotto di $A$ per $C$) -relativamente alla scelta dei punti $O$ e $I$- nella seguente maniera:

1.
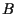sia $B$ un punto non giacente su $l$,
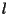2.
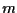sia $m$ la retta passante per 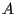$A$ e parallela a $l(I,B)$,
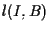3.
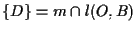poniamo $\{D\}=m\cap l(O,B)$,
4.
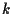sia $k$ la retta passante per 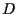$D$ e parallela alla retta $l(B,C)$,
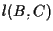5.
definiamo 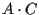$A\cdot C$ come il punto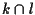 $k\cap l$


5. OSSERVAZIONE Si vede subito che i passaggi effettuati sono ben posti anche se a priori il punto $A\cdot C$ dipende dalla scelta di $B$.
Come per l'addizione, $B$ è detto punto ausiliario nella definizione di $A\cdot C$ e chiaramente, una volta fissato, $D$ da esso è univocamente determinato; useremo ancora la locuzione "moltiplichiamo $A$ e $C$ usando $B$ (e $D$)".

Mostriamo che il punto $A\cdot C$ è indipendente dalla scelta $B$:
siano $B_1,B_2$ due punti non giacenti su $l$; calcoliamo il prodotto di $A$ per $C$ utilizzando $B_1$ (e $D_1$) e $B_2$ (e $D_2$); denotiamo il risultato rispettivamente con $(A\cdot C)_1$ e $(A\cdot C)_2$.
A questo punto distinguiamo due casi:
  • I CASO
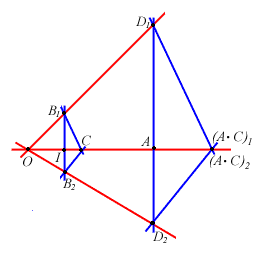
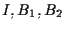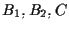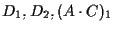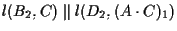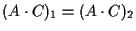    $I,B_1,B_2$ collineari: applicando il Teorema di Desargues ai triangoli $B_1,B_2,C$ e $D_1, D_2,(A\cdot C)_1 $ otteniamo che $l(B_2,C)\parallel l(D_2,(A\cdot C)_1)$ e questo implica $(A\cdot C)_1 =(A\cdot C)_2$.
  • II CASO
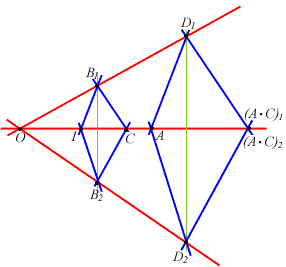
    lasciamo al lettore i dettagli
    (si osservi la figura adiacente e si ricordi come si è proceduto nel caso dell'addizione -clicca qua per il confronto).


In definitiva abbiamo una ben definita operazione interna su $l$ (relativamente alla scelta di $O$ e $I$).

MAPPA DEL SITO ______ vai in cima alla pagina_______________ precedente__ successivo________________________