

 |
 |
 |
 |
 |
 |
 |
 |

|

|
1. DEFINIZIONE ADDIZIONE SULLE RETTE DI UN PIANO AFFINE DESARGUESIANO
Sia
Definiamo il punto
- sia
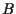 un punto non giacente su
un punto non giacente su 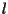 ,
,
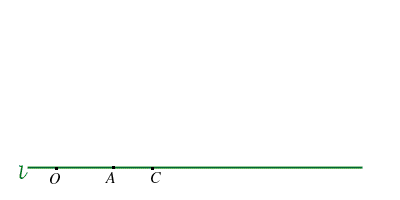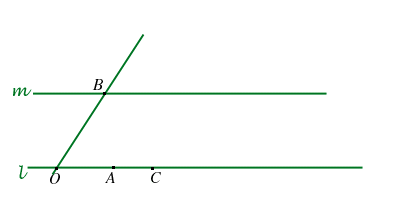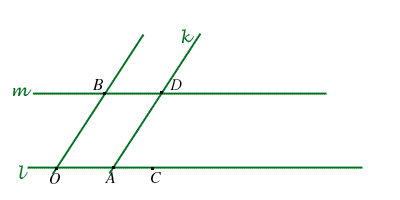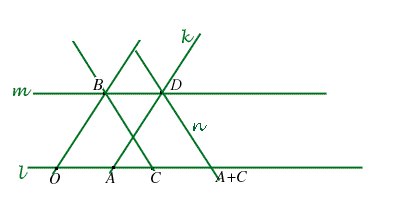
- sia
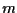 la retta per
la retta per 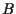 parallela a
parallela a 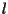 ,
,
- sia
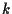 la retta per
la retta per 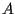 parallela alla retta
parallela alla retta 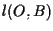 ,
, -
poniamo
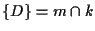 ,
,
- sia
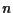 la retta passante per
la retta passante per 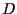 e parallela alla retta
e parallela alla retta 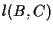 ,
,
- definiamo
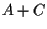 come il punto
come il punto 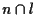 .
.
2. OSSERVAZIONE A priori comunque il punto
Il nostro compito è ora mostrare che
Siano
A questo punto si distinguono due casi:
- I CASO:
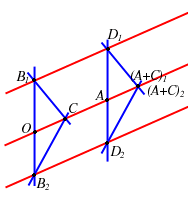
 collineari; l'assioma delle parallele ci assicura che anche i punti
collineari; l'assioma delle parallele ci assicura che anche i punti 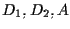 sono allineati lungo la retta passante per
sono allineati lungo la retta passante per 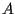 e parallela a
e parallela a 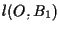 .
.
Ora usando il Teorema di Desargues relativamente ai triangoli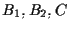 e
e
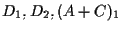 otteniamo che
otteniamo che
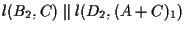 .
.
Ma noi sappiamo che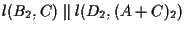 e di qui segue necessariamente che
e di qui segue necessariamente che
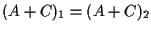 .
.
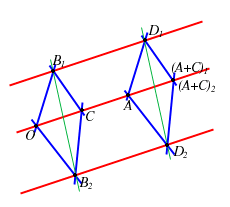
- II CASO:
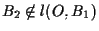 ;
utilizzando il Teorema di Desargues relativamente ai triangoli
;
utilizzando il Teorema di Desargues relativamente ai triangoli 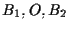 e
e 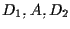 otteniamo che
otteniamo che
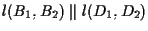 ed utilizzando ancora il Teorema di Desargues questa volta relativamente ai triangoli
ed utilizzando ancora il Teorema di Desargues questa volta relativamente ai triangoli 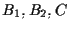 e
e
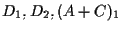 otteniamo che otteniamo che
otteniamo che otteniamo che
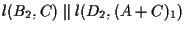 e come in I CASO possiamo concludere che
e come in I CASO possiamo concludere che
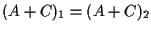 .
.
In definitiva abbiamo che l'addizione di punti di una retta affine

 _______________
_______________
 __
__
 ________________________
________________________