

 |
 |
 |
 |
 |
 |
 |
 |

|

|
3. PROPOSIZIONE Sia
DIMOSTRAZIONE
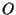 elemento neutro:
elemento neutro: 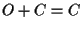 e
e 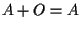

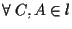 .
.
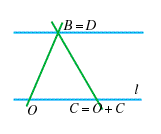 Per la prima uguaglianza si osservi che, seguendo le notazioni di definizione 1, in cui ora
Per la prima uguaglianza si osservi che, seguendo le notazioni di definizione 1, in cui ora 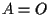 si ottiene di conseguenza che
si ottiene di conseguenza che 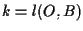 e
e 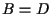 ,
otteniamo
,
otteniamo 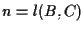 e dunque
e dunque 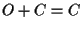 .
.
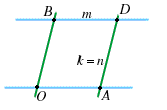 Per la seconda uguaglianza si ha che
Per la seconda uguaglianza si ha che
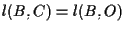 cosicché
cosicché 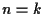 ;
poiché
;
poiché 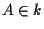 e
e
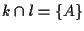 , allora si ha che
, allora si ha che 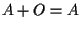 .
.
- esistenza dell'opposto:
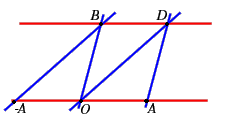
 esiste un unico punto di
esiste un unico punto di  ,
che denoteremo
,
che denoteremo  ,
tale che
,
tale che
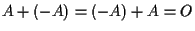 .
.
Infatti sia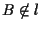 e
e
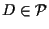 tale che
tale che
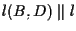 e
e
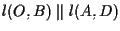 come nella definizione di addizione; sia per definizione
come nella definizione di addizione; sia per definizione 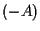 il punto di intersezione della retta
il punto di intersezione della retta 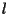 con la retta passante per
con la retta passante per 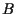 e parallela a
e parallela a 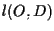 (queste due rette non possono essere parallele!); sommando
(queste due rette non possono essere parallele!); sommando 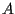 e
e 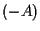 con
con 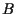 come punto ausiliario (e necessariamente è
come punto ausiliario (e necessariamente è 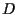 il secondo punto ausiliario) otteniamo proprio
il secondo punto ausiliario) otteniamo proprio 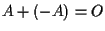 ;
l'altra uguaglianza si ottiene invece sommando
;
l'altra uguaglianza si ottiene invece sommando 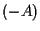 e
e 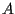 con
con 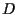 (e
(e 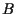 )
come punto ausiliario.
)
come punto ausiliario.
- associatività della somma:
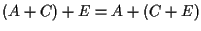

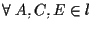 .
.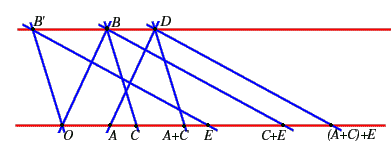
Calcoliamo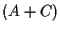 utilizzando
utilizzando 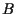 (e
(e 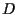 )
come punto ausiliario e poi sommiamo
)
come punto ausiliario e poi sommiamo 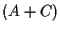 ad
ad 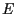 utilizzando un punto
utilizzando un punto 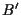 scelto sulla retta
scelto sulla retta 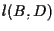 in modo tale che
in modo tale che
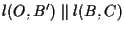 . Questo forzerà il punto
. Questo forzerà il punto  ad essere il secondo punto ausiliario anche in questo caso e cosí otteniamo
ad essere il secondo punto ausiliario anche in questo caso e cosí otteniamo
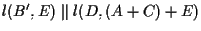 .
.
Ora sommiamo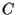 ed
ed 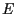 utilizzando
utilizzando
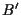 (e
(e 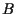 )
e infine sommiamo
)
e infine sommiamo 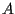 e
e 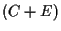 usando
usando 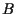 (e
(e 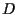 ). Questo implica
). Questo implica
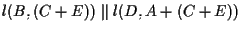 .
.
Poiché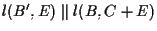 l'assioma delle parallele ci assicura che i punti
l'assioma delle parallele ci assicura che i punti 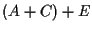 e
e 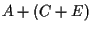 coincidono.
coincidono.
- commutatività della somma:

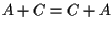

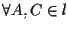 .
.
Sommiamo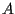 e
e 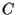 utilizzando
utilizzando 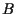 (e
(e 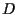 )
e poi calcoliamo
)
e poi calcoliamo 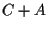 utilizzando sempre
utilizzando sempre 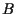 come punto ausiliario (e determinando cosí un secondo punto ausiliario
come punto ausiliario (e determinando cosí un secondo punto ausiliario 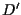 ).
).
Poiché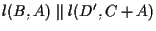 ,
seguirà che i punti
,
seguirà che i punti 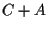 e
e 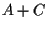 coincideranno se riusciremo a far vedere che
coincideranno se riusciremo a far vedere che
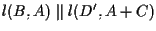 .
.
E a tal fine usiamo il Teorema di Desargues B relativamente alle terne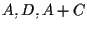 e
e 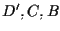 e otteniamo che le rette
e otteniamo che le rette 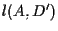 ,
,
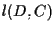 e
e 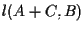 sono parallele o concorrenti.
sono parallele o concorrenti.
A questo punto possiamo usare il Teorema di Desargues sulle terne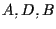 e
e 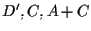 per ottenere proprio che
per ottenere proprio che
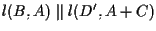 .
.

 _______________
_______________
 __
__
 ________________________
________________________