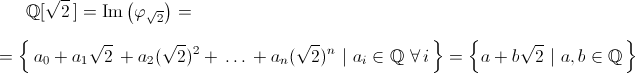Estensioni di campi - 2

Morfismo di valutazione. Siano A e B anelli, A sottoanello di B, e sia u un fissato elemento di B. Come è facile verificare l'applicazione di valutazione in u, φ_u : A[x]→B con φ_u(f)=f(u), è un morfismo di anelli, conserva infatti somma, prodotto ed elemento neutro del prodotto.

Sottoanello generato da A e da u. Per il teorema fondamentale di omomorfismo per gli anelli si ha, tra A[x]/Ker(φ_u) ed Im(φ_u), l'isomorfismo di anelli che ad f+Ker(φ_u) associa f(u). L'immagine del morfismo di valutazione Im(φ_u)={f(u) | f∈A[x]} è un sottoanello di B detto sottoanello generato da A e da u e denotato con A[u]. Esso è il piu piccolo anello che contiene sia A che u ed è inoltre l'intersezione di tutti i sottoanelli di B che contengono sia A che u.

Esempio 1. Consideriamo l'estensione di campi R/Q e sia u=√2. Allora, il morfismo di valutazione in √2 è: φ_√2 : Q[x]→R, φ_√2(f)=f(√2). L'immagine di φ_√2 risulta:

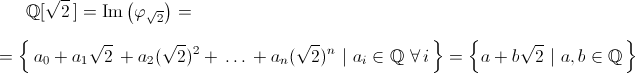Esempio 2. Sia Z l'anello degli interi, sottoanello del campo dei razionali Q, e sia 1/3∈Q. In questo caso φ_1/3 :Z[x]→Q, φ_1/3(f)=f(1/3) e l'immagine è:

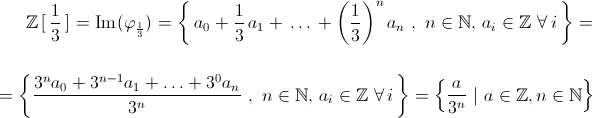Guardiamo cosa succede nel caso particolare dei campi. Sia F/K estensione di campi e sia u∈F. Come sopra, l'applicazione di valutazione in u φ_u : K[x]→F, φ_u(f)=f(u) è un morfismo di anelli e:

$K[u]=\text{Im}(\varphi_u)=\left\{f(u)\vert{f\in K[x]}, {u\in F}\right\}$

è un sottoanello del campo F.

Il nucleo di φ_u è un ideale di K[x] e non coincide mai con K[x] in quanto nessun polinomio costante diverso da 0 di K[x] si annulla in u.

Essendo K[x] (anello dei polinomi nell'indeterminata x con coefficienti nel campo K) un dominio euclideo, esso è necessariamente anche un dominio ad ideali principali (PID), dunque deve esistere un suo elemento h che da solo generi l'ideale Ker(φ_u).

Si hanno dunque due casi:

φ_u iniettiva se e solo se Ker(φ_u)=(0), quindi se e solo se u è trascendente su K

φ_u non iniettiva se e solo se Ker(φ_u)≠(0), quindi se e solo se u è algebrico su K.

In questo caso esiste un unico polinomio di K[x] monico e tale che l'ideale da esso generato coincida con Ker(φ_u). Questo polinomio è detto polinomio minimo di u su K e si denota con p_u. Esso dipende da F/K e dalla scelta di u in F.

Ogni polinomio a coefficienti in K che si annulla in u appartiene all'ideale (p_u) e dunque ha p_u come divisore.

Lemma. Se u∈F è algebrico su K, p_u è l'unico polinomio monico ed irriducibile in K[x] che si annulla in u.

Indietro - Avanti

Esercizi

Home