Estensioni di campi - 3

Decidere se un polinomio in K[x] è irriducibile su K può essere difficile. Ecco qualche strumento.

Criterio di Eisenstein. Sia f∈Z[x], f=f₀+f₁x+...+f_nxⁿ con f_n≠0. Se esiste un numero primo p tale che p non divide f_n, p divide f₀,...,f_n-1 e p² non divide f₀, allora f è irriducibile su Q.

Lemma. Sia f∈K[x]. Se deg(f)=1,  f  è irriducibile. Se deg(f)=2 o 3, f è irriducibile se e solo se non ha radici in K.

Esempio 1. Sia R/Q e.c. e sia √2=u∈R. L'elemento u è algebrico (su Q) perchè esiste il polinomio x²-2∈Q[x] che si annulla in u. Esso è inoltre il polinomio minimo in quanto è monico e irriducibile su Q perchè è di secondo grado con tutte le radici in R e non in Q.

Esempio 2. Sia C/R e.c. e sia i∈C. Come sopra i è algebrico su R perchè esiste x²+1∈R[x] che si annulla in i. Esso è il polinomio minimo: è monico e irriducibile su R perchè è di secondo grado con tutte le radici in C e non in R.

Consideriamo una torre di campi, cioè K⊆F⊆E con F/K ed E/F estensioni di campi e quindi anche E/K estensione di campi.

Sia u∈F, allora il polinomio minimo su K di u pensato come elemento di F coincide con il polinomio minimo su K di u pensato come elemento di E.

Invece se v∈E, il polinomio minimo di v su K è in generale diverso dal polinomio minimo di v su F. Ad esempio: Q⊆R⊆C; sia u=√2∈R; allora il polinomio minimo di u relativo all'estensione R/Q è x²-2, come quello relativo all'estensione C/Q. Invece se pensiamo a √2∈C, il polinomio minimo su R è x-√2, su Q è x²-2.

Infatti:

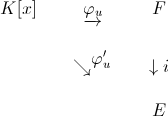
con: ker(φ_u)=ker(φ'_u)=(p_u).

Grado di un elemento algebrico. Sia F/K e.c. e sia u∈F algebrico su K. Il grado di u su K è il grado di p_u.
Se u∈F ed u è algebrico su K, u ha grado 1 se e solo se u∈K infatti p_u ha grado 1 se e solo se p_u=x-u∈K[x].

Indietro - Avanti

Esercizi

Home