Estensioni di campi - 4

Sottocampo generato da K e da u. Siano F/K e.c. e u∈F. Poichè K[u]⊆F, K[u] è un dominio e questo implica l'esistenza di un campo dei quozienti Q(K[u]) per K[u]. Per la proprietà universale del campo dei quozienti si ha un morfismo (necessariamente iniettivo) di campi ψ da Q(K[u]) ad F. L'immagine di ψ è un sottocampo di F isomorfo a Q(K[u]). Tale campo è detto sottocampo di F generato da K e da u e si denota con K(u).
K(u) è il più piccolo sottocampo di F contenente K come sottocampo ed u come elemento ed è quindi l'intersezione di tutti i sottocampi di F che contengono K come sottocampo ed u come elemento. Si ha:

K(u) è il più piccolo sottocampo di F che contiene K[u].

Se u è algebrico su K, si ha che K[u] è isomorfo a K[x]/(p_u) che è un campo, quindi, se u è algebrico, K(u)=K[u]. Se u è trascendente, K(u) è isomorfo a K(x).

Sottocampo generato da K e da u₁,...,u_n. Siano F/K e.c. ed u₁,...,u_n∈F. Posto:

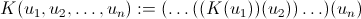
K(u₁,...,u_n) è il piu piccolo sottocampo di F contenente K ed u₁,...,u_n ed è intersezione di tutti i sottocampi di F che contengono K ed u₁,...,u_n. Esso è chiamato sottocampo di F generato da K e da u₁,...,u_n e non dipende dall'ordine in cui si considerano u₁,...,u_n.
K(u₁,...,u_n) è il campo dei quozienti del dominio K[u₁,...,u_n], definito:

Siano K(u₁,...,u_n)/K e K(v₁,...,v_m)/K estensioni di campi; K(u₁,...,u_n)⊆K(v₁,...,v_m) se e solo se u₁,...,u_n∈K(v₁,...,v_m) e quindi K(u₁,...,u_n)=K(v₁,...,v_m) se solo se u₁,...,u_n∈K(v₁,...,v_m) e v₁,...,v_m∈K(u₁,...,u_n).