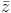)∈R[x])Estensione
finita di campi. Grado di un'estensione finita di campi.
Sia F/K estensione di campi, allora F
è spazio vettoriale su K
con la moltiplicazione per scalari data
dal prodotto interno di F. Se la dimensione di F
come K-spazio vettoriale è finita, F/K
si dice estensione
finita di campi (F estensione
finita di K). In questo caso la dimensione di F
su K si dice grado dell'e.c. e
si denota con [F:K].
Sia K⊆F⊆E
una torre di campi,
allora F è K-sottospazio vettoriale di E e, se E/K
è estensione finita di campi, si ha: [F:K]≤[E:K].
Sia F/K e.c., allora [F:K]=1
se e solo se F=K.
Sia F/K e.c. e sia u∈F, allora u è algebrico su K se e solo se K(u)/K è estensione finita di campi. In questo caso, n=[K(u):K] è il grado di u su K, ovvero è pari al grado di pu e una base per K(u) su K è data da {1,u,u2,...,un-1}. K(u) è infatti isomorfo a K[x]/(pu) che ha base {1,ξ,ξ2,...,ξn-1} dove ξ è la classe di equivalenza [x].
Sia F/K e.c. e sia u∈F, allora K[u] e K(u) sono K-spazi vettoriali.
Esempio 1. C/R è estensione finita di campi, essendo C un R-spazio vettoriale di dimensione 2 (una base è {1,i}).
Esempio 2. Q[√2]/Q è estensione finita di campi, essendo Q[√2] un Q-spazio vettoriale di dimensione 2 (una base è {1,√2}).
Esempio 3. Q[∛2]/Q è estensione finita di campi di grado 3, con base {1, ∛2, ∛4}.
Estensioni algebriche e trascendenti. Sia F/K e.c., F è una estensione algebrica di K se ogni elemento di F è algebrico su K. In caso contrario F è una estensione non algebrica o estensione trascendente di K.
Esempio 1. Consideriamo il sottocampo Q(π) di R; Q(π) è estensione trascendente di Q.Lemma. Sia F/K estensione finita di campi, allora ogni elemento di F è algebrico su K ed il grado su K di ogni elemento di F è minore o uguale di [F:K]. Segue che F/K è e.c. algebrica.
Esempio 1. C/R è e.c. finita di grado [C:R]=2 e dunque, per il corollario, è algebrica. Sia ora z∈C, il grado di z su R è minore o uguale di 2 ed in particolare è: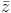)∈R[x])Lemma della Torre. Consideriamo la torre di campi K⊆F⊆E, cioè siano E/F ed F/K e.c.. Allora F/K è estensione finita se e solo se E/F ed F/K sono estensioni finite.
Se F/K è finita, si ha [E:K]=[E:F]·[F:K]; inoltre, se {u1,...,un} è una base di F su K, e {v1,...,vs} è una base di E su F, allora una base di E su K è data da {u1v1,u1v2,...,u1vs,...,unv1,...,unvs}.
Lemma. Sia F/K e.c. e siano u1,...,un∈F algebrici su K. Allora K(u1,...,un) è estensione finita di campi.
Lemma. Sia F/K e.c. e siano u,v∈F algebrici su K. Allora u+v, u·v, -u e, se u≠0, u-1 sono algebrici su K.
Lemma. Siano F/K e.c., u∈F, f∈F[x] non nullo. Sia f=f0+f1x+...+fnxn con f0,...,fn algebrici su K allora, se f(u)=0, u è algebrico su K.
Campi di spezzamento. Siano K un campo, f∈K[x], deg(f)>0. Un campo di spezzamento di f su K è una estensione di campi E/K tale che su E si abbia:
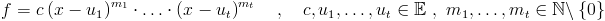
e tale che E=K(u1,...,ut).
Esempio 1. Il campo di spezzamento di x2+1 su R è C mentre il campo di spezzamento di x2-1 su R è R.