Estensioni di campi - 1

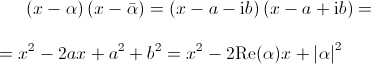
Ricordiamo alcune definizioni ed alcuni risultati (quasi sempre senza dimostrazioni) sulle estensioni di campi.

Estensione di campi. Siano K ed F campi, K sottocampo di F. Allora F/K è un'estensione di campi (brevemente F/K e.c.).

Esempio 1. Notiamo che Q è sottocampo di R il quale è a sua volta sottocampo di C, quindi si ha che R/Q, C/R e C/Q sono estensioni di campi.

Elementi algebrici e trascendenti. Sia F/K estensione di campi, u∈F, u è detto algebrico su K se esiste f∈K[x] diverso dal polinomio nullo e tale che f(u)=0; u è detto trascendente su K in caso contrario.

Esempio 1. Consideriamo l'estensione di campi C/R; per ogni a,b∈R si ha che α=a+ib∈C è radice del polinomio di secondo grado in x (x-α)(x-ᾱ):

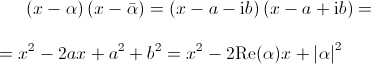
che è a coefficienti reali, da cui ogni numero complesso è algebrico sul campo reale.

Esempio2. Sia F/K e.c., si ha che tutti gli elementi di K sono algebrici su K infatti per ogni u∈K il polinomio x-u∈K[x] si annulla in u.

Numeri algebrici e trascendenti. Consideriamo l'estensione di campi C/Q; un numero complesso u è un numero algebrico se è algebrico su Q, numero trascendente altrimenti.

Esempio 1. I numeri reali √2, √3, 2 (e così pure -√2, -√3, -2) sono algebrici in quanto radici dei polinomi a coefficienti razionali x²-2, x²-3 ed x-2 rispettivamente.

Se n∈N, n>0 e a,b∈R, b>0, il polinomio x²ⁿ⁺¹-a ha esattamente una radice reale, che viene denotata con , e il polinomio x²ⁿ-b ha esattamente due radici reali, di cui quella positiva viene denotata con . Dunque i numeri reali  e sono algebrici.

Esempio 2. Il numero complesso 2-3i è algebrico essendo radice del polinomio razionale x²-4x+13.

Esempio 3. I numeri reali π ed e sono numeri trascendenti: la dimostrazione di questo fatto non è banale.

Avanti

Esercizi

Home