L'insieme dei numeri reali  R

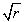    Abbiamo visto che la divisione è divenuta un'operazione possibile in Q (a parte l'impossibilità di dividere per 0). Consideriamo adesso un' altra operazione:  l’estrazione di radice quadrata.  Dato un elemento generico r appartenente a Q definiamo la radice quadrata di r:

Definizione:  Sia  r  Q, un elemento  t Q  tale che   t ²= r  si dice radice quadrata di  r, e si indica con  .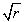

    Questa operazione non è sempre possibile; ad esempio si ha ovviamente che se  r  < 0,  nessun numero t Q può soddisfare la relazione  t= r,  poiché  t²   è comunque un numero positivo.   Ma anche quando  r  > 0, non è detto esista t Q  con  t² = r . 
Vediamolo nel caso di  r = 2.

Teorema:  Non esiste nessun numero razionale, che elevato al quadrato dia 2 .

Dimostrazione:   Dobbiamo vedere che non esiste nessun   t Q, tale che:

t² = 2

    Supponiamo per assurdo che esista un elemento razionale della forma  t = a/b, e (riducendo ai minimi termini) possiamo supporre che a e b siano primi tra loro, che soddisfi l’equazione scritta sopra.   Allora  l’espressione diventa (a/b) = 2,  che è equivalente a scrivere
a² /b² = 2 ,  o ancora:

    Notiamo inanzitutto  a e b non possono essere entrambi pari perché  altrimenti avrebbero un fattore comune, il 2 , e la frazione non sarebbe ridotta ai minimi termini.

Ma a e b  non possono essere neanche entrambi dispari perché il termine 2b² sarebbe sempre pari e il termine a² dispari.

Quindi da ciò si deduce che a deve essere pari e b dispari .

    Se b è dispari anche b²  lo è , quindi il termine  2b²  contiene il fattore 2 solo una volta. Invece a  è pari  e contiene il fattore 2 almeno una volta, cioè si può scrivere:  a =  2c , quindi    a² = 4c² , e quindi   a²  contiene  il fattore 2  almeno due volte!

    Quindi, concludendo, non si può avere  a² = 2b² , e ciò significa che non esiste nessun elemento della forma a/b , che elevato al quadrato ci dà 2.

    Geometricamente ciò come si traduce?  In un quadrato con un lato di lunghezza 1, se applichiamo il teorema di Pitagora per calcolare la lunghezza della sua diagonale non otteniamo un numero razionale!  

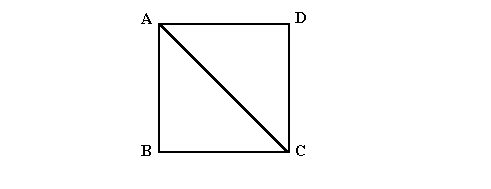
    Iinfatti applicando il teorema di Pitagora al triangolo  ABC, si ottiene   (AB)² + (BC)² = (AC)² ,  ma  (AB)² + (BC)² = 1+ 1 = 2, e quindi la misura di  AC  deve essere un numero che elevato al quadrato fa 2, ed abbiamo appena dimostrato che cioà eà impossibile per un numero razionale.

    Questo fatto ci mostra che ci sono lunghezze di segmenti che non corrispondono a numeri razionali, cioè che se vogliamo associare ad ogni punto di una retta un numero,  non bastano i razionali per "riempire la retta", ma che dovremo ampliare l'insieme numerico che consideriamo.

    Cerchiamo di definire gli elementi mancanti , riprendendo il problema di trovare un numero che al quadrato faccia 2.  Possiamo considerare dei numeri decimali finiti che approssimino  per difetto oppure per eccesso la quantità  cercata.

        Consideriamo i numeri:    1 ; 1,4  ;  1,41  ;   1,414 ; ……  (cioè i razionali che elevati al quadrato  danno un valore  < 2),

        E poi i numeri:                2 ;  1,5 ;  1,42 ;  1,415 ; ………  (cioè i razionali che elevati al quadrato danno un valore  > 2).

    Chiamiamo R, insieme dei numeri reali, l'insieme ottenuto, cioè quello ove abbiamo tutti i possibili decimali finiti ed infiniti, periodici (razionali) o meno (irrazionali).  Rappresentano ad esempio dei numeri reali (irrazionali) espressioni come:

dove la "legge" con si succedono le cifre è chiara, ma non c'è periodicità.

    In R si possono definire le operazioni analoghe a quelle che avevamo in Q , ed esse godranno ancora delle proprietà citate negli insiemi precedenti, inoltre R è completo cioè “non ci sono buchi”: se riportiamo i numeri reali sulla retta, ad ogni punto della retta corrisponde uno di essi e viceversa.

In  R si ha poi la seguente proprietà, che non si aveva in  Q  :

     Cioè in  R è sempre eseguibile l'operazione di radice quadrata dei numeri positivi, dove per "radice quadrata di r ³ 0" , si intende un numero positivo che moltiplicato per se stesso dia  r .  Tale numero si indica con 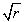. Anzi , per ogni r > 0, esistono due numeri che elevati al quadrato danno r : e cioè   ± .
 

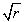    Più in generale, per ogni numero naturale n > 0, si definisce l'operazione di radice n-esima di un numero reale r ³ 0 , come quel numero, se esiste, che elevato alla  n  dà   r . In simboli:   .

    Non è invece eseguibile in R la radice quadrata dei numeri negativi; infatti ogni numero reale elevato al quadrato risulta sempre positivo; un'espressione come 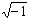non ha alcun senso in  R.