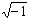Cenni sui numeri complessi,  C.

    L'ultima estensione del "campo dei numeri" (a cui accenniamo soltanto) è quella nella quale rendiamo possibile l'estrazione di radice quadrata di numeri negativi.  L'ampliamento rispetto all'insieme dei reali avviene essenzialmente attraverso l'introduzione di un  solo nuovo "numero", il numero  i , detto "unità immaginaria"  il quale ha la proprietà:

 
              i2= -1

Praticamente abbiamo quindi aggiunto ai numeri reali una  .

    Definiamo l'insieme dei  Numeri complessi, C, come l'insieme delle espressioni del tipo a+ib , ove a,b siano numeri reali,  ed i è quella che abbiamo denotato come unità immaginaria.
     Nell'espressione di un numero complesso  z = a+ib,   a  viene detta  parte immaginaria  di z  e  b  parte reale  di z .
   
    Le operazioni di somma e prodotto in  C si svolgono secondo le regole usuali del calcolo letterale, ma  tenendo conto che  i2= -1; ad esempio:

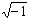(12 + i) + (1+4i) = 13 + 5i   ;   (2+3i)(1-i)  =  2 -2i +3i -3i2 =  2 + i - (- 3) = 5 + i ;

(2+i)(2-i)  =  4 - i2 =  4 - (-1)  = 5  ;   [(1+i)/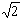]2 = (1+i)2/2 =  (1-1+2i)/2  =  i .


     Per rappresentare geometricamente i numeri complessi una retta non basta più; avremo invece bisogno di un piano:

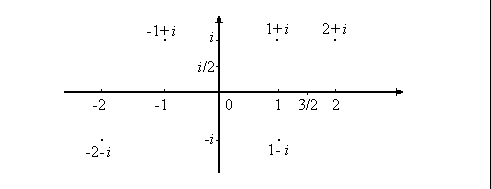
    I numeri reali si vedono "dentro" i complessi sull'asse orizzontale della figura (asse reale), mentre sull'asse verticale appariranno i numeri immaginari puri (e cioè  i, 2i, 5i, -3i ; tutti quelli della forma ai, dove a è un numero reale).

    Anche in  C varranno le proprietà delle operazioni che avevamo in R , ne avremo inoltre altre come il fatto che nei numeri complessi ogni equazione polinomiale (di qualsiasi grado) ha soluzioni, ed ogni numero possiede due radici quadrate, tre radici cubiche, quattro radici quarte, e così via.

Esempi:

    Se   z2= -25 ,  allora  z =  ±5i ;   se   z2= -2 ,  allora  z = 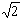 ±i .

    Se   z3= -1,  allora i possibili valori di  z sono:  

            z1 = -1 ,  z2 = (1+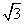i)/2 ,   z3 = (1-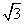i)/2   (queste sono le 3 radici cubiche dell'unità).

    Se   z4= -1,  allora   z1 = 1 ,  z2 = -1 ,  z3 = i ,   z4 = -i   (queste sono le 4 radici quarte dell'unità).

 
 
                                                                                                   ESERCIZI                                          Home page