ELEMENTI DI TEORIA INGENUA DEGLI INSIEMI
INDICE:
Nozioni preliminari, Notazioni.
Operazioni tra insiemi.
Partizioni ed Insieme quoziente.
Nozioni preliminari, Notazioni.
Penseremo un insieme come
una "collezione" di oggetti (in generale facente parte di un fissato
universo di discorso). Un insieme può essere espresso in
due modi :
1) elencandone tutti gli elementi ;
2) fornendo una proprietà che caratterizza i suoi elementi.
In generale si usano parentesi graffe per denotare insiemi; ad esempio, con la
notazione di tipo 1):
A = {a , e , i , o , u} , B = {3 , 41 , 5 , 1 , 2}
indicano l’ insieme delle
vocali, A, ed un
insieme B che ha come elementi i numeri 3
, 41 , 5 , 1 , 2 (gli insiemi vengono in genere indicati con una lettera
maiuscola).
La notazione di tipo 1) è ovviamente possibile soltanto per insiemi finiti e
non ad esempio per l’ insieme dei numeri naturali N, per il quale si può comunque usare una notazione come:
dove l'utilizzo dei puntini è il mezzo per ovviare
all'impossibilità di scrivere infiniti elementi.
Useremo questo artificio quando la successione
di elementi che costituiscono l'insieme prosegue in modo ovvio. La scrittura
precedente è da non confondere
naturalmente con l’ insieme {0 , 1 , 2, 3} che ha invece solo 4 elementi.
Altri
esempi :
C = {
![]() }
,
D = {+, - , : ,
}
,
D = {+, - , : ,
 }.
}.
Il secondo modo per specificare un insieme è mostrato dai seguenti esempi:
A= {x naturale | x
< 5 } o B = {x naturale | x è dispari e x < 8}.
Questo rappresenta un altro modo per specificare gli elementi di un insieme, visti nel modo 1), gli elementi dell’ insieme A sono 1,2,3,4 mentre quelli dell’ insieme B sono 1,3,5,7.
Un insieme particolare è l’insieme vuoto,
un insieme che non contiene nessun elemento. Esso è indicato con il simbolo: 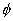 .
.
Per indicare che un elemento a appartiene ad un insieme A si usa il simbolo
"![]() ", scrivendo
a
", scrivendo
a
![]() A ; ad esempio se consideriamo l’insieme B = {3 , 41 , 5 , 1 , 2}, possiamo scrivere che
41
A ; ad esempio se consideriamo l’insieme B = {3 , 41 , 5 , 1 , 2}, possiamo scrivere che
41 ![]() B.
B.
Se invece un
elemento x non appartiene ad un insieme A si usa il simbolo
![]() , scrivendo
x
, scrivendo
x
![]() A .
A .
Definizione: Se abbiamo due insiemi A e B tali che ogni elemento dell’ insieme B sta anche in A, diremo che B è un sottoinsieme di A , scrivendo B
![]() A .
A .
Ad esempio se A = {1,2,3,5} e B = {1,2}, allora B
![]() A . Invece l’insieme C =
{1,2,4} non è un sottoinsieme di A e si usa il seguente modo per indicarlo: C
A . Invece l’insieme C =
{1,2,4} non è un sottoinsieme di A e si usa il seguente modo per indicarlo: C
![]() A.
A.
Definizione: Due insiemi A e B sono uguali se ogni elemento di A è anche elemento di B e, viceversa, ogni elemento di B è anche elemento di A.
Esempi:
1) A = {2 , 5 , 6 , 7} ; B = {5 , 6 , 7 , 2}
sono uguali perché ogni elemento di A è elemento di B e viceversa.
2) C = {3 , 4 , 5 , 6 , 8} ; D = {3 , 4 , 8 , 6 , 2}
non sono uguali, ad esempio 5 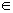 C , ma 5
C , ma 5 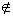 D .
D .
Possiamo osservare dai due esempi che quando scriviamo un insieme, non
ha importanza l'ordine in cui scriviamo i suoi elementi.
Operazioni tra insiemi.
Considereremo le seguenti operazioni fra insiemi:
Definizione: Dati due insiemi A e B, si dice unione di A e B l'insieme A
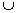 B che contiene sia gli elementi di
A che di B, cioè:
B che contiene sia gli elementi di
A che di B, cioè:
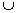 B = {x tali che x
B = {x tali che x 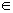 A oppure x
A oppure x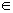 B }.
B }.
Esempio:
A ={1 , 2 , 3} , B ={3 , 5 , 7}
L’ unione è
A
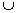 B = {1 , 2 , 3 , 5 ,
7}
B = {1 , 2 , 3 , 5 ,
7}
 B che contiene sia gli elementi comuni ad
A e a B, cioè:
B che contiene sia gli elementi comuni ad
A e a B, cioè:  B = {x tali che x
B = {x tali che x
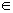 A e x
A e x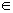 B }.
B }.
Esempio
G = {2 , 4 , 3} , F = {2 , 6 , 3}
G  F = {2 , 3}
F = {2 , 3}
L’ intersezione tra due insiemi può essere anche vuota, ad esempio:
A = {
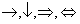 } e
B = {
} e
B = { }
}
A
 B =
B = 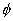
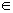 A e x
A e x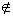 B }.
B }.Esempio
A = {1 , 3 ,5 , 6 } , B = {1 , 3 , 4}
La differenza è l’ insieme A \ B = {5 , 6} .
Notiamo che (al contrario di unione ed intersezione) la differenza non
é un'operazione commutativa, infatti
utilizzando la definizione abbiamo nell'esempio precedente: B \ A = {4} .
Diamo una rappresentazione visiva di queste operazioni fra insiemi:
Se:
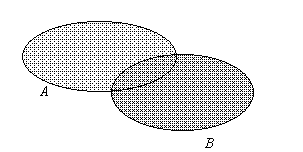
allora:

 B = {(x,y) tali che x
B = {(x,y) tali che x
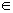 A e y
A e y 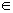 B }.
B }.Esempio:
A = {1 , 2 , 3} , B = {5 , 6 , 3 , 1}
A  B = {(1 ,5), (1 , 6) , (1 , 3) , ( 1 , 1) , (2 , 5) , ( 2 ,
6) , (2 , 3) , (2 , 1) , (3 , 5), (3 , 6) , (3 , 3) , (3 , 1) }
B = {(1 ,5), (1 , 6) , (1 , 3) , ( 1 , 1) , (2 , 5) , ( 2 ,
6) , (2 , 3) , (2 , 1) , (3 , 5), (3 , 6) , (3 , 3) , (3 , 1) }
Notiamo che anche il prodotto
cartesiano non è commutativo, cioè A  B è diverso
da B
B è diverso
da B  A , ad esempio:
A , ad esempio:
B  A = {(5 , 1) , (5 , 2)
, (5 , 3) , (6 , 1) , (6 , 2) , (6 , 3) , (3 , 1) , (3 , 2) , (3 , 3) , (1 , 1)
, (1 , 2) , (1 , 3)}
A = {(5 , 1) , (5 , 2)
, (5 , 3) , (6 , 1) , (6 , 2) , (6 , 3) , (3 , 1) , (3 , 2) , (3 , 3) , (1 , 1)
, (1 , 2) , (1 , 3)}
Partizioni ed Insieme quoziente.
Dato un insieme A, consideriamo una famiglia di suoi sottoinsiemi che ne dà una suddivisione; più precisamente, se la famiglia di sottoinsiemi verifica le due proprietà seguenti :
1) l’ unione di tutti questi sottoinsiemi ricopre A;
2) non ci sono elementi comuni tra due o più classi,
allora la famiglia di sottoinsiemi di A si dice una partizione di A ed i suoi sottoinsiemi vengono detti classi di partizione.
La situazione è illustrata nella seguente figura:

Data una partizione di un insieme A, è utile definire un nuovo insieme detto insieme quoziente, che si ottiene prendendo come elementi le classi stesse della partizione.
Ad esempio nel caso della figura sopra l’ insieme quoziente è B = {A 1 , A2 , A3 , A4 , A5 }, cioè l’insieme delle classi.
Esempio:
Consideriamo l‘insieme dei giocatori di calcio di serie A ; la suddivisione
le cui classi sono ottenute raggruppando tutti i giocatori di una stessa
squadra formano una partizione dell’ insieme totale. In questo caso, l’ insieme quoziente è
C = {Juventus , Milan , Bologna , Lazio ……..}
e cioè l’ insieme delle squadre di serie A, che rappresentato le classi della partizione.
Il concetto di Funzione fra Insiemi.
Insiemi numerici.
Esercizi Torna su Home Page


