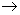 B
BFUNZIONI FRA INSIEMI
Vediamo adesso un concetto molto importante in matematica, quello di funzione.
Quella che segue è una definizione un po' intuitiva di che cosa si
intende per funzione:
Definizione: Dati due insiemi A e B si dice funzione (o anche applicazione) da A a B una legge
che ad ogni elemento dell’ insieme A associa uno ed un solo elemento di B .
In genere le funzioni si indicano con le
lettere minuscole; per indicare che f è una funzione da A a B si scrive
|
f : A
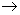 B B |
Se abbiamo una funzione f: A
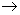 B ed a
B ed a
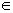 A , sia b
A , sia b
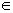 B l’elemento di B associato all’elemento a dalla f
; allora diremo che
B l’elemento di B associato all’elemento a dalla f
; allora diremo che
"la f porta a in b", e scriveremo in simboli: f(a) = b.
Vediamo due esempi tramite una
rappresentazione visiva:

Le due figure qui sopra illustrano due esempi di funzioni : nel primo caso gli insiemi
A ={a1,a2,a3} e B ={b1,b2,b3}
hanno tre elementi ciascuno e la funzione porta ogni elemento ai di A nell’elemento bi di B (ove i = 1,2,3 ), cioè f(ai) = bi .
In questo esempio la legge f è una funzione: ad ogni ai si associa uno ed un solo elemento di B , cioè bi.
Nel secondo esempio gli insiemi sono gli stessi, ma ora la funzione porta gli elementi a1
e a2 in b1 e l’elemento a3 in b2 ,
mentre nessuno elemento di A viene portato in b3. Anche questo è un esempio di funzione, notiamo che nulla vieta
che una funzione porti due o più elementi di A in uno stesso elemento di B.
Consideriamo altri due esempi in figura:

Entrambe le leggi illustrate non sono funzioni perché nella prima figura all’elemento a3 non è associato nessun elemento di B , mentre nella seconda l’elemento a1 viene portato
sia in b1 che in b2 , mentre la definizione di
funzione ci dice che si deve associare ad ogni elemento di A uno ed un solo elemento di B.
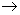 Y . Allora diremo
immagine di X (tramite f), o anche immagine di f, l’ insieme
Y . Allora diremo
immagine di X (tramite f), o anche immagine di f, l’ insieme 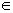 Y | esiste x
Y | esiste x 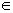 X , con y = f(x)} .
X , con y = f(x)} . Analogamente, se A è un sottoinsieme di X , diremo immagine di A (tramite f):
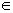 Y | esiste x
Y | esiste x 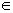 A , con y = f(x)}.
A , con y = f(x)}. Y . Sia B
Y . Sia B 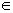 X | f(x)
X | f(x) 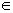 B }
B }
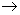 Y ; essa si dice
suriettiva se f(X) = Y
cioè se l'immagine di f è tutto Y .
Y ; essa si dice
suriettiva se f(X) = Y
cioè se l'immagine di f è tutto Y .
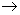 Y ;
essa si dice iniettiva se
Y ;
essa si dice iniettiva se
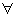 x1 , x2
x1 , x2 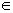 X si ha :
X si ha :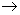 Y che sia suriettiva ed iniettiva si dice biunivoca (o anche biettiva o bigettiva).
Y che sia suriettiva ed iniettiva si dice biunivoca (o anche biettiva o bigettiva).
Le funzioni che ci interessano sono quelle fra insiemi
numerici, per vedere qualche esempio:
Esercizi Home Page