Funzioni fra insiemi numerici:   Esempi e Grafici.

Considereremo qui funzioni del tipo   f : X 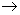Y ( rappresentata dalla scrittura generica y = f(x), intendendo che la f  associa al generico elemento x 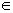X  l'elemento  y 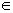Y ), ove  X ed  Y  siano insiemi numerici.

La variabile  x varia su un insieme X  (il dominio) e prende il nome di variabile indipendente perché può assumere qualsiasi valore ivi fissato. Invece la variabile y prende il nome di variabile dipendente  perché dipende dal valore dato alla  x .


    Negli esempi che andremo a vedere, considereremo sempre x ed y nell'inseme  R  dei numeri reali.

Esempio 1.   Sia    f : X 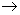Y , ove la   f   è definita da  y =1/x  ,  e   y, x  siano numeri reali.

Per questa funzione  possiamo stabilire come dominio l'insieme di tutti i valori di  R tranne lo 0 ,  perché la quantità  1/x  non avrebbe  nessun senso per   x = 0,  quindi il massimo dominio X  ove la  f  è definibile rappresentato da X = R/{0} .  

    Ricordiamo che per grafico della funzione, intendiamo il sottoinsieme G del prodotto cartesiano  X x Y  dato dall'insieme delle coppie  (x,y), ove sia y = f(x), cioè:    G = {(x,y) 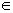X x Y | y = f(x) } .
    Possiamo così rappresentare il grafico delle funzioni date su insiemi di numeri reali nel piano cartesiano, cioè nel piano euclideo ove si siano fissate due assi coordinate perpendicolari su cui riportare i valori della x (asse delle ordinate, orizzontale) e della y (asse delle ascisse, verticale).

Riprendendo il nostro esempio  y =1/x , il grafico sarà:

---

Esempio 2.   Sia    y = .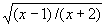

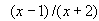Definiamo quale può essere il dominio: dobbiamo avere che  deve essere positivo (o nullo) e ciò accade per valori della x  dati da:  x < - 2  ed  x ³ 1.

Quindi il dominio è rappresentato dall’ insieme:   {x 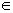R | x <-2  oppure   x ³ 1}  (in rosso nella figura sotto).

Vediamo il grafico :

---

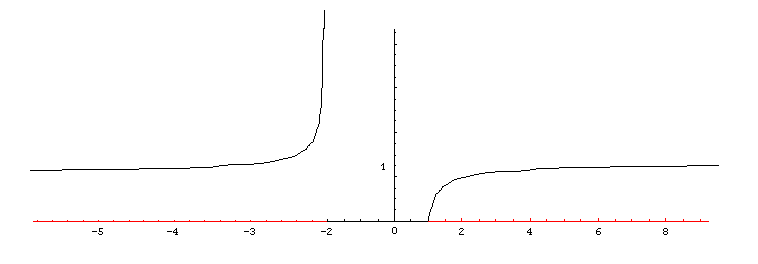
        Notiamo che non tutte le espressioni che si scrivono in modo simile ad y=f(x) sono date da funzioni; ad esempio, se consideriamo

    l’ espressione: 

y =

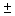
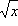
essa non rappresenta una funzione,  perché ad ogni valore di  x corrispondono due valori di  y  ( considerando x ³ 0 ).

    Si può comunque tracciare il grafico dato dalle coppie (x,y)  che soddisfano l'espressione sopra:

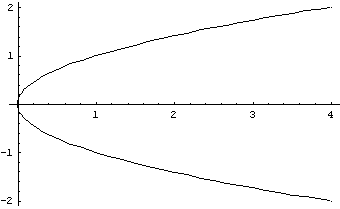
    Possiamo pensare questa figura  come il grafico di due funzioni:  la funzione data da:   y = 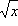(arco superiore della parabola) e quella data da  y = - 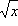(arco inferiore).

---

    Si ha invece una parabola che è data da una funzione considerando l'espressione:

y = x

questa è una funzione perché ad ogni un dato x corrisponde uno ed uno solo y :

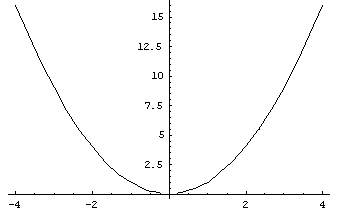
    Notiamo che questa funzione  vista come   f : R 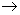R  non è suriettiva perché se consideriamo una  y di valore negativo, ad esempio y = -1 , non otterremo alcun valore di x per il quale  f(x) = -1, quindi l'immagine di f non è tutto R, in effetti abbiamo:

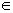 im f =  R₊  = {x R | x ³ 0}

    Considerando la funzione come  f : R 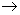R₊ ,  allora la  f  è suriettiva.  In  ogni caso essa non risulta iniettiva, in quanto,  ad esempio,

f(-2) =   f(2) =  4 .

---