Teoria Generale
In questa sezione daremo la definizione ed esporremo i principali risultati riguardanti le serie numeriche. Sarà utile avere familiarità con il concetto di "limite" e quello di "successione". Entrambe queste nozioni infatti compaiono direttamente nella definizione di serie e risultano fondamentali per comprendere pienamente il concetto di "convergenza" che rappresenta il fulcro di tutta la trattazione.
Definizioni
Sia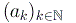 
una
successione
di numeri reali.
Si chiama serie numerica associata a tale successione, la scrittura formale:
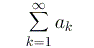
Si chiama invece somma parziale n-esima il numero reale Sn ovvero:
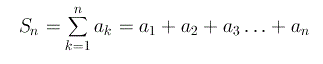
Diremo poi che la serie converge, diverge o oscilla se rispettivamente converge, diverge o oscilla la successione delle somme parziali.
Dunque risulta chiaro che una serie è convergente se il limite della successione delle somme parziali esiste finito, è divergente se tale limite esiste ma è infinito mentre oscilla se la successione delle somme parziali non ammette limite.
Se esiste il limite per n che tende ad infinito di Sn, tale limite si chiama somma della serie e si pone per definizione:
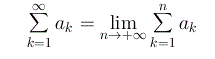
Diremo infine che una serie converge assolutamente se converge la serie dei moduli cioè se esiste finito
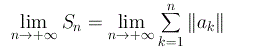
Teoremi
Linearità
"Date due serie convergenti, la serie che ha per successione una combinazione lineare delle due successioni di partenza, è convergente."
La dimostrazione utilizza la definizione di convergenza e la proprietà distributiva del prodotto rispetto alla somma.
Condizione di Cauchy
Rappresenta l'analogo per le serie della nota condizione di Cauchy sulla convergenza delle successioni. Anche in questo caso tale condizione è necessaria e sufficiente e potremmo esprimerla così:
"Una serie numerica reale è convergente se preso un indice n abbastanza grande e presi due interi m e r tali che m > r > n, l'elemento m-esimo e l'elemento r-esimo della successione delle somme parziali risultino arbitrariamente "vicini" tra loro."
La dimostrazione
segue direttamente dalla definizione di convergenza e dalla
completezza sequenziale di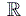 
.
Corollario
Dal teorema di Cauchy segue un utile corollario la cui dimostrazione è immediata e viene lasciata al lettore:
"Affinché una serie converga è necessario (ma non sufficiente) che il termine n-esimo tenda a zero al crescere di n."
Assoluta convergenza
"Ogni serie assolutamente convergente è anche convergente."
La dimostrazione utilizza la disuguaglianza triangolare, la definizione di convergenza assoluta e la condizione di Cauchy.
Comportamento delle serie a termini positivi
"Una serie a termini positivi o è convergente o è divergente."
La dimostrazione segue dai teoremi sui limiti di successioni monotone.
Esempi
Serie Armonica semplice
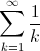
Tale serie è una serie a termini reali positivi e non è convergente poiché non verifica la condizione di Cauchy ergo è divergente. Si noti che, in questo caso, la divergenza è indipendente del fatto che il termine n-esimo tenda a zero o meno. Questo mostra chiaramente la non sufficienza di tale condizione.
Serie Armonica generalizzata
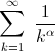
Anche questa serie è a termine reali positivi e utilizzando il
criterio integrale
mostreremo che tale serie converge soltanto se il parametro reale
è strettamente maggiore di uno.
Serie Geometrica
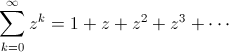
Tale serie è detta serie geometrica di ragione z, dove z è un opportuno numero reale (o complesso) fissato. Mostreremo di seguito che tale serie risulta convergente soltanto se |z|<1.
Supponiamo di fissare z=1, allora la successione delle somme parziali Sn vale esattamente n. Valutandone il limite avremo:
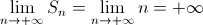
che è proprio la definizione di serie divergente.
Sia adesso z un qualsiasi reale diverso da uno. Allora possiamo moltiplicare entrambi i membri dell'equazione per (1-z) ottenendo:
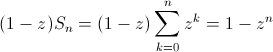
da cui, spostando (1-z) al denominatore, in quanto non nullo, e passando al limite per n che tende ad infinito abbiamo:
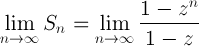
ed ovviamente tale limite esiste finito se e solo se la successione zn è convergente e questo accade soltanto se |z|<1.
Serie Telescopica
Si definisce telescopica una serie in cui "contano" solo il primo e l'n-esimo termine poiché gli altri si elidono vicendevolmente. Utilizzando l'usuale notazione formale chiameremo telescopica una serie del tipo seguente:
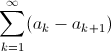
Proprio per come è definita, una serie di questo tipo
converge se e solo se converge la successione
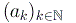e in tal caso la somma della serie vale:
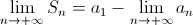
Una celebre serie telescopica è la serie di Mengoli:
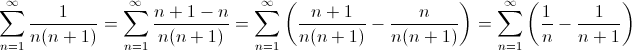
tale serie ha ovviamente somma uno in quanto la successione 1/n è infinitesima per n che tende ad infinito.