Assoluta convergenza
Ipotesi:
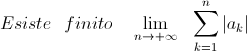
Tesi:
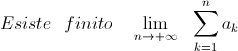
Dimostrazione:
Se una serie è assolutamente convergente, significa che la serie dei moduli verifica la condizione di Cauchy ovvero:
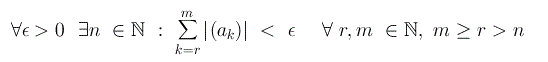
Dalla disuguaglianza triangolare (il valore assoluto di una somma è minore o uguale della somma dei valori assoluti) si ha:

che sostituita nella condizione precedente ci fornisce direttamente
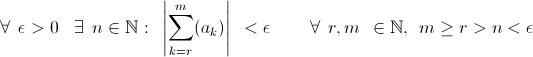
e quindi la serie data è anche semplicemente convergente proprio per il teorema di Cauchy.
