Introduzione
Lo studio delle serie numeriche è stato introdotto in matematica per generalizzare l'operazione di addizione al caso in cui si desideri effettuare la somma di un numero infinito di elementi. Il concetto di somma infinita è molto antico ed uno degli esempi più celebri è forse quello conosciuto come "Paradosso di Zenone" o anche come "Achille e la Tartaruga".
Achille e la Tartaruga
Achille detto "piè veloce" viene sfidato ad una gara di corsa da una tartaruga e per rendere la gara più equa, decide di concedere alla sua avversaria un po' di vantaggio. L'argomentazione di Zenone è la seguente: se Achille concedesse anche solo un piede di vantaggio alla tartaruga, non riuscirebbe mai a raggiungerla poiché, nel tempo necessario ad Achille a coprire la distanza che li separa, la sua avversaria, seppur lentamente, si sarà mossa guadagnando un po' di terreno, e nel tempo in cui Achille coprirà il nuovo "gap", ancora una volta la tartaruga si sarà spostata in avanti cosicché sebbene la distanza tra i due si riduca costantemente essa diverrà zero solo in un tempo infinito. Zenone allora conclude che semplicemente il "sorpasso di Achille" non possa avvenire, in netto contrasto con quanto l'esperienza quotidiana ci suggerisce. L'argomentazione di Zenone appare ineccepibile eppure noi sappiamo che l'eroe greco è certamente più veloce di una tartaruga e quindi non solo egli la supererà in un tempo finito ma certamente arriverà anche per primo alla meta, indipendentemente dal vantaggio concesso alla sua sfidante. Com'è dunque possibile che due ragionamenti apparentemente corretti e coerenti portino a risultati diametralmente opposti? Vediamo nel dettaglio un esempio pratico e cerchiamo di capire come sia possibile sciogliere il paradosso di Zenone.
La velocità di Achille (va) è 5 m/s
(supponiamola costante)
La velocità della Tartaruga (vt) è invece 0,5 m/s
(anch'essa costante e irrealistica)
Achille concede alla Tartaruga 9 m di vantaggio
Ora una semplicissima applicazione della cinematica classica, nel caso di un moto rettilineo uniforme unidimensionale, ci fornisce la seguente relazione tra spazio, tempo e velocità:
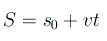
dove con S indichiamo lo spazio, con s lo spazio iniziale, con v la velocità e con t il tempo. Quindi uguagliando la legge oraria relativa al moto di Achille e la legge oraria relativa al moto della tartaruga otteniamo l'equazione nell'incognita t:
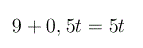
Da cui, ricavando t, scopriamo che dopo soli due secondi Achille raggiungerà la tartaruga e tale sorpasso avverrà a dieci metri dalla linea di partenza. Ora, con gli stessi dati, cerchiamo di seguire il ragionamento di Zenone: il filosofo sostiene che nel tempo impiegato da Achille a coprire i nove metri la tartaruga si sarà spostata un po' più avanti, dunque per prima cosa dobbiamo ricavare il tempo t, utilizzando come dati, nella legge oraria sopra citata, la velocità di Achille e il vantaggio concesso alla tartaruga. Otterremo così

Nel tempo t1 la tartaruga copre la distanza S2
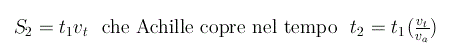
In questo secondo intervallo di tempo la tartaruga si sposta nuovamente
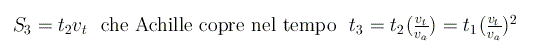
e così via. Dunque siamo di fronte ad una somma infinita di elementi, ognuno dei quali è progressivamente più piccolo del precedente in quanto il rapporto tra le due velocità è minore di uno. Come già detto, Zenone conclude che, essendo una somma infinita di tempi, essa non può avere per soluzione un tempo finito. Ma ecco che emerge la potenza dell' argomentazione analitica, in grado di sciogliere come neve al sole il paradosso del filosofo greco. Infatti, grazie al concetto di convergenza di una serie, noi sappiamo che una infinita somma di elementi infinitesimi può avere un risultato finito. La somma dei tempi necessari per il sorpasso di Achille è la seguente:
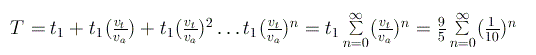
Come mostreremo più avanti tale serie è detta serie geometrica di ragione 1/10 ed è una serie a termini positivi, convergente, con somma:
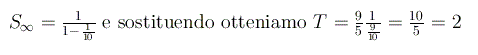
che è proprio quanto avevamo trovato uguagliando le due leggi orarie.
