Serie Numeriche

Criteri di convergenza

In questa sezione sono riportati alcuni utili strumenti teorici per valutare il carattere di una serie data. In generale, non è detto che i teoremi qui presentati siano immediatamente ed universalmente applicabili alla serie che si desidera studiare. È quindi molto importante fare attenzione alle ipotesi che compongono i successivi enunciati, in modo da utilizzare tali criteri opportunamente, evitando così di giungere a conclusioni errate.

Criterio del confronto

È il criterio più versatile e permette di stimare la convergenza di una serie confrontandola con un'altra il cui carattere è noto.

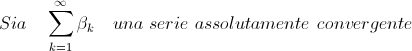
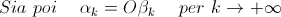
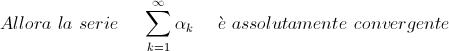
Ovviamente nel caso di serie a termini reali positivi possiamo sostituire l'ipotesi di convergenza assoluta con quella di convergenza semplice.

Criterio della radice

Consideriamo una generica serie a termini reali o complessi

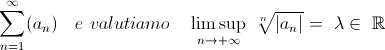
Allora avremo che se tale limite superiore è minore di uno, la serie converge assolutamente, se invece è maggiore di uno allora la serie non converge. Nulla si può dire se il limite vale esattamente uno.

Criterio del rapporto

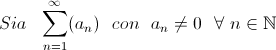
Supponiamo esista

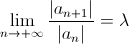
Se 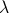< 1 la serie converge assolutamente.

Se 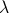> 1 la serie non converge.

Se 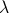= 1 il criterio è inefficace.

Criterio integrale

Sia 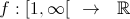una funzione continua, non negativa e monotona decrescente. Si ha:

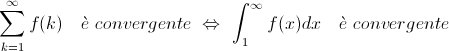
Esempio celeberrimo: Serie armonica generalizzata

Criterio di Abel-Dirichlet

Sia 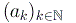una successione in 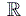a termini positivi, monotona decrescente e che tenda a zero per n che tende all'infinito. Sia poi 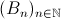una successione tale che risulti limitata la successione delle somme parziali S_n ovvero

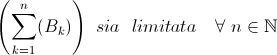
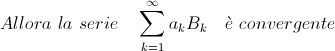
Criterio di Leibnitz

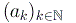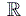Se è una successione in monotona decrescente e che tende a zero per n che tende all'infinito, allora la serie

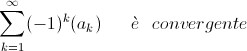
Criterio di Raabe-Duhamel

Supponiamo di esaminare una serie a termini reali positivi tale che:

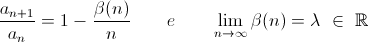
Se 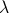> 1 la serie converge.

Se 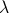< 1 la serie non converge.