Teorema di Cauchy
Ipotesi:
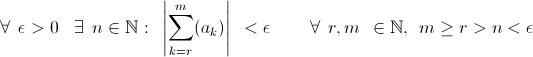
Tesi:
Tale condizione è necessaria e sufficiente per la convergenza della serie
Dimostrazione:
Per definizione una serie è convergente se e solo se la successione delle somme parziali ha limite finito
e ciò significa che tale successione ha per punto di accumulazione un numero reale o in altre parole essa è
convergente come successione a tale numero reale. Essendo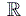 
sequenzialmente completo
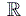(ovvero ogni successione di Cauchy in è convergente), la serie data converge
se e solo se la successione delle somme parziali è una successione di Cauchy e quindi risulta:
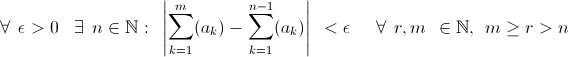
che è esattamente quanto si voleva provare.