template

Il gruppo diedrale di ordine 2 n è il gruppo formato dalle isometrie del piano che lasciano immutati i poligoni regolari a n lati .

L'aggettivo diedrale deriva da diedro (dal greco: solido a due facce), che a sua volta origina dalla possibilità di considerare un poligono come un solido degenere ad altezza nulla.

Gli elementi del gruppo diedrale

Gli elementi base del gruppo sono le rotazioni del poligono pari all'n-esima parte dell' angolo giro , e la riflessione attorno ad un asse di simmetria del poligono. Esistono in tutto n rotazioni possibili e n assi di simmetria per un poligono di n lati, per cui il gruppo diedrale corrispondente è formato da 2 n elementi.

Una rotazione del pentagono di $\frac{360^\circ}{5}=72^\circ=\frac{2 \pi}{5}\mbox{rad}$

Una riflessione del pentagono attorno al proprio asse di simmetria

Indicato con r la rotazione di $\frac {2 \pi}{n}$ radianti in senso antiorario, e s la riflessione attorno ad uno degli assi di simmetria, valgono le seguenti relazioni:

r n = 1 : dopo n rotazioni si ritorna sui vertici di partenza;
s 2 = 1 : due riflessioni consecutive si annullano;
r k s = s r n - k : in particolare, il gruppo non è commutativo ;
ogni simmetria si può ottenere come composizione di s e di un adeguato numero di rotazioni r ;
la composizione di due rotazioni o due riflessioni è una rotazione; la composizione di una rotazione e una riflessione è una riflessione.

Segue che è possibile generare tutto il gruppo da r ed s ; in alternativa, poiché due riflessioni consecutive sono uguali ad una rotazione, si può generare il gruppo a partire da due riflessioni s 1 e s 2 (pertanto il gruppo diedrale è di Coxeter ).

Un rotazione si può ottenere come la composizione di due riflessioni

[ modifica ] Definizioni equivalenti

pagina principale

È possibile dare per il gruppo diedrale numerose definizioni equivalenti alla precedente:

è il gruppo con presentazione

$\langle r, s \mid r^n = 1, s^2 = 1, srs = s^{-1} \rangle$ oppure $\langle s_1, s_2 \mid s_1^2 = s_2^2 = (s_1 s_2)^n = 1 \rangle$ ;

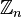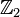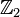è il prodotto semidiretto dei gruppi ciclici $\mathbb{Z}_n$ e $\mathbb{Z}_2$ , con $\mathbb{Z}_2$ che agisce su 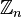$\mathbb{Z}_n$ per inversione;

[ modifica ] Proprietà

per 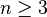$n \geq 3$ , D n è un sottogruppo del gruppo simmetrico S n ;
dato un numero m che divide n , D n ha $\frac{n}{m}$ sottogruppi di tipo D n e un sottogruppo di tipo 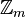$\mathbb{Z}_m$ ;

[ modifica ] Proprietà che dipendono dalla parità dei lati

Gli assi di simmetria di un poligono sono disposti in maniera diversa, a seconda che il numero dei suoi lati sia pari (metà degli assi passano per i vertici e metà passano per il centro dei lati) oppure dispari (ogni asse passa per un vertice e il centro del lato opposto). Questo comporta che alcune delle proprietà del gruppo diedrale associato possono variare a seconda della parità di n :

il centro del gruppo, ovvero l'insieme degli elementi che commutano con tutto il gruppo, è formato dalla sola identità se n è dispari, mentre contiene anche l'elemento $a^{\frac{n}{2}}$ se n è pari.

se n è dispari, tutte le riflessioni appartengono alla stessa classe di coniugio ; se invece n è pari esistono due classi di coniugio separate: le riflessioni attorno agli assi passanti per i vertici e quelle attorno agli assi passanti per i lati non sono collegabili fra di loro mediante rotazioni.

[ modifica ] Gruppi diedrali piccoli

Il caso n = 1 è considerato degenere e non è menzionato da molti autori; si può considerare come il gruppo composto dalla sola rotazione di 2p e dalla simmetria lungo una qualunque retta; corrisponde al gruppo 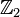$\mathbb{Z}_2$ .

Il caso n = 2 (simmetrie del piano che lasciano invariato un 2-agono, cioè un segmento ) è generato dalla rotazione di p e dalla riflessione attorno all'asse del segmento. Queste due trasformazioni, pur essendo identiche sui i punti del segmento, non lo sono per l'intero piano. Il gruppo è isomorfo a $\mathbb{Z}_2 \times \mathbb{Z}_2$ (gruppo di Klein ).

D 1 e D 2 sono gli unici gruppi diedrali commutativi.

[ modifica ] Gruppi diedrali e radici dell'unità

L'insieme delle radici n-esime dell'unità , dato da

$\left\{ r_k = \cos \frac{2\pi k}{n} + i \sin \frac{2\pi k}{n} :\, k = 0,\,1,\, \ldots,\,n-1 \right\} \subseteq (\mathbb{C})$

sul piano complesso corrisponde ai vertici di un poligono a n lati. La moltiplicazione per r 1 corrisponde alla rotazione di $\frac {2 \pi}{n}$ , mentre l'operazione di coniugazione complessa $\overline{x + iy} = x - iy$ corrisponde alla riflessione lungo l'asse reale. Segue che il gruppo generato a partire da queste due operazioni, con l'operazione di composizione, è il gruppo diedrale di ordine n .

[ modifica ] Generalizzazioni

[ modifica ] Gruppo diedrale infinito

Il gruppo diedrale ha tra i suoi generatori una rotazione a che è un multiplo razionale dell'angolo giro, per cui esiste sempre un intero n per cui a n è l'identità, e il gruppo generato è di ordine finito; se invece consideriamo rotazioni che non sono multiple razionali di 2p , non esiste alcuna loro potenza che sia l'identità; segue che il gruppo generato (indicato con $D_\infty$ ) ha infiniti elementi.

La sua presentazione è data da $\langle r, s \mid s^2 = 1, srs = r^{-1} \rangle$ oppure $\langle s_1, s_2 \mid s_1^2 = s_2^2 = 1 \rangle$ .

[ modifica ] Gruppo diedrale generalizzato

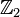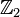Dato un gruppo commutativo H , il gruppo diedrale generalizzato di H , che si indica con D( H ) , è il prodotto semidiretto di H e di $\mathbb{Z}_2$ , con $\mathbb{Z}_2$ che agisce su H per inversione.

Valgono cioè le regole di moltiplicazione:

$\begin{matrix} \forall h_1 ,\, h_2 \in H ,\, t_2 \in \mathbb{Z}_2 : \\ (h_1, 0) \cdot (h_2, t_2) &=& (h_1 + h_2, t_2) \\ (h_1, 1) \cdot (h_2, t_2) &=& (h_1 - h_2, 1 + t_2) \end{matrix}$

Poiché $\mbox{D}(\mathbb{Z}_n) = \mbox{D}_n$ e $\mbox{D}(\mathbb{Z}) = \mbox{D}_\infty$ , questa definizione estende quella di gruppo diedrale di un poligono. Gli elementi del tipo ( h ,0) corrispondono alle rotazioni e formano un sottogruppo normale di D( H ) isomorfo ad H , mentre gli elementi del tipo ( h ,1) corrispondono alle riflessioni.