 |
| Introduzione |
| Isometrie nello spazio |
| Solidi platonici |
| Simmetrie dei solidi platonici |
| Bibliografia |
Riflessioni
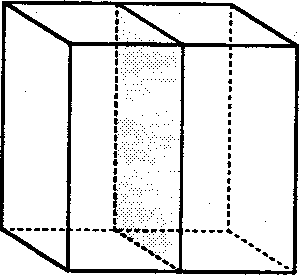
Per individuare le riflessioni bisogna trovare i piani di simmetria del cubo, che sono in tutto nove:
 |
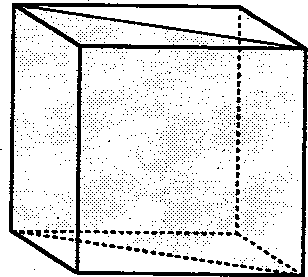 |
| Tre piani paralleli a due facce opposte | Sei piani contenenti due spigoli opposti |
Abbiamo quindi 9 riflessioni.
Riflessioni rotatorie
Bisogna trovare tutte le possibili composizioni di una riflessione con una rotazione (diversa dall'identità) che riportano il cubo in se stesso ed escludere i casi che si ripetono.
La prima di tali simmetrie che si incontra viene chiamata applicazione antipodale, ed è la simmetria rispetto all'origine, cioè l'applicazione che porta un punto A dello spazio nel punto diametralmente opposto ad A rispetto all'origine. Questa simmetria porta ogni vertice nel vertice opposto ed è data dalla composizione di una riflessione di arbitrario piano di simmetria per l'origine e da una rotazione di angolo 180° ed asse ortogonale al piano scelto.
Tutte le altre riflessioni rotatorie si cercano a partire dalle rotazioni del gruppo già studiate, scartando però tutte quelle quelle di angolo 180° in quanto componendole con una riflessione si ritornerebbe al caso dell'applicazione antipodale.
 |
