Studiamole quindi a partire dagli assi di rotazione possibili e tenendo conto che il piano di simmetria delle riflessioni deve essere perpendicolare a tali assi:

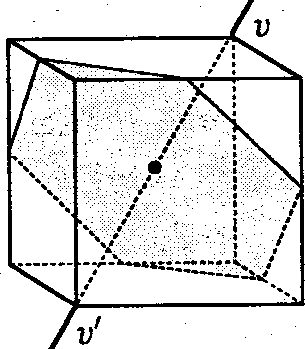
Caso1_ Asse per due vertici opposti (v, v')	il piano di riflessione è un piano che taglia il cubo secondo un esagono regolare ed ha vertici nei punti medi dei sei spigoli non adiacenti a v, v'. Le rotazioni possibili sono quelle di 120°, 240°. Sono quindi in tutto 8 possibili simmetrie.
Caso 2_ Asse per i punti medi di due spigoli opposti	l'unica rotazione possibile era quella di 180° , quindi tale caso viene scartato
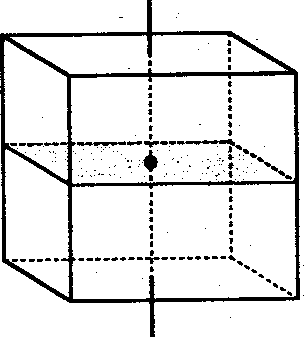
Caso 3_ Asse che congiunge i centri di due facce opposte	Il piano di riflessione è parallelo alle due facce e, scartando nuovamente la rotazione di 180°, rimangono quindi la rotazione di 90° e quella di 270°. Sono in tutto 6 possibili simmetrie.

Tenendo conto dell'applicazione antipodale abbiamo in tutto 15 riflessioni rotatorie