

 |
 |
 |
 |
 |
 |
 |
 |

|
Convenzione: affermando che
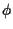 di corpi che fa corrispondere ad un punto
di corpi che fa corrispondere ad un punto Come sempre ci riferiremo ad esempio al corpo
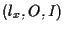 piú semplicemente come a
piú semplicemente come a
Sia
![]() un piano affine desarguesiano con assi fissati
un piano affine desarguesiano con assi fissati ![]() .
.
Vogliamo far vedere che ogni retta ![]() di
di
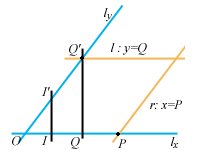
![]() è costituita da tutti e soli i punti
è costituita da tutti e soli i punti 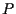 le cui coordinate
le cui coordinate 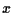 ,
,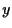 soddisfano ad una qualche equazione lineare del tipo
soddisfano ad una qualche equazione lineare del tipo
![]() con
con ![]() elementi del corpo
elementi del corpo ![]() e
e ![]() non entrambi nulli (e diremo piú brevemente che
non entrambi nulli (e diremo piú brevemente che ![]() ha come equazione
ha come equazione
![]() o equivalentemente che
o equivalentemente che ![]() soddisfa l'equazione
soddisfa l'equazione
![]() )
e viceversa mostreremo che un'equazione di questo tipo individua una retta di
)
e viceversa mostreremo che un'equazione di questo tipo individua una retta di
![]() (probabilmente il lettore è stato abituato a scrivere i coefficienti di un'equazione come la precedente a destra, ma a noi torna piú comodo scriverli a sinistra e siccome in piano affine desarguesiano ma non pappiano la moltiplicazione fra punti non è commutativa non si tratta di una differenza a priori di poco conto).
(probabilmente il lettore è stato abituato a scrivere i coefficienti di un'equazione come la precedente a destra, ma a noi torna piú comodo scriverli a sinistra e siccome in piano affine desarguesiano ma non pappiano la moltiplicazione fra punti non è commutativa non si tratta di una differenza a priori di poco conto).
3. OSSERVAZIONI Poiché, come osservato, i punti
 Poiché analogamente tutti i punti di una retta
Poiché analogamente tutti i punti di una retta  al punto
al punto
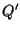 di intersezione tra
di intersezione tra Identicamente le rette parallele alla retta
Per mostrare che i punti di ogni retta soddisfano una certa equazione lineare ci servono alcuni risultati preliminari.
4. PROPOSIZIONE Sia
Sia
Allora vale
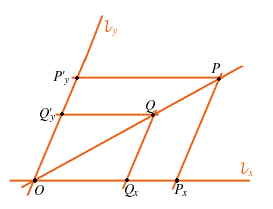
DIMOSTRAZIONE Basta usare il Teorema di Desargues applicato alle terne
Grazie alla proposizione precedente possiamo associare ad ogni retta per
5. PROPOSIZIONE Sia
Sia
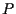 le cui coordinate
le cui coordinate 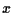 ,
,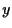 soddisfano l'equazione lineare
soddisfano l'equazione lineare
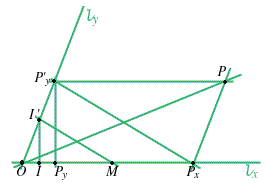
DIMOSTRAZIONE Sia
Poiché
Poiché evidentemente anche
Quanto fatto non ci garantisce che non ci siano altri punti in
Vogliamo far vedere che questo non accade:
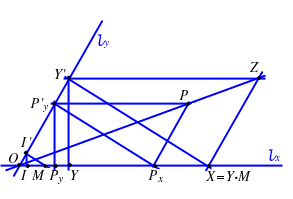
siano
Sia
Altrimenti, calcolando
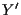 ,
otteniamo che
,
otteniamo che 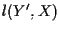 è parallela a
è parallela a
Ora applicando il Teorema di Desargues B alle terne
Poiché quindi
6. PROPOSIZIONE Sia
Sia
Sia
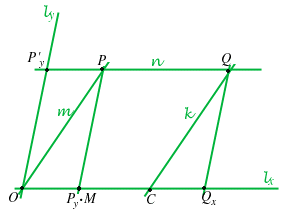
DIMOSTRAZIONE Sia
Calcoliamo la somma
Possiamo compendiare i risultati ottenuti nell'enuciato del seguente teorema:
7. TEOREMA Sia
- se
 è una retta e
è una retta e
 allora
allora  soddisfa l'equazione
soddisfa l'equazione 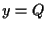 ove
ove 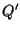 è il punto di intersezione di
è il punto di intersezione di 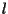 con
con 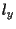 ,
,
- se
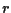 è una retta e
è una retta e
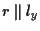 allora
allora 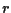 soddisfa l'equazione
soddisfa l'equazione 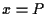 ove
ove 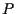 è il punto di intersezione di
è il punto di intersezione di 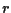 con
con 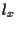 ,
,
- se
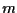 è una retta e
è una retta e 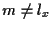 ,
,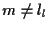 e
e 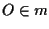 allora
allora 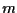 soddisfa l'equazione
soddisfa l'equazione
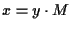 ove
ove 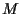 è il punto già descritto in precedenza,
è il punto già descritto in precedenza,
- se
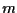 come sopra e
come sopra e 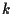 è una retta tale che
è una retta tale che
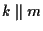 ,
,
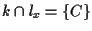 ,
allora
,
allora 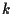 ha equazione
ha equazione
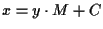 .
.
Chiaramente ogni retta rientra in uno e uno solo dei casi contemplati.
8. COROLLARIO Sia
![]() un piano affine desarguesiano (risp. pappiano), sia
un piano affine desarguesiano (risp. pappiano), sia ![]() una retta in
una retta in
![]() e
e ![]() due punti distinti su
due punti distinti su ![]() e
sia
e
sia
![]() il corpo (risp. campo)
il corpo (risp. campo) ![]() ;
allora
;
allora
![]() è identificabile con il piano affine coordinato
è identificabile con il piano affine coordinato
![]() .
.
DIMOSTRAZIONE È il contenuto di teorema 7 e di teorema 2

 _______________
_______________
 __
________________________
__
________________________