|
|
2. TEOREMA
Sia
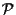 un piano affine desarguesiano (risp. pappiano); siano
un piano affine desarguesiano (risp. pappiano); siano 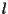 una retta e
una retta e 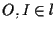 due punti distinti; sia
due punti distinti; sia
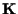 il corpo (risp. campo)
il corpo (risp. campo) 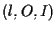 ;
allora esiste una corrispondenza biunivoca tra ;
allora esiste una corrispondenza biunivoca tra
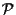 e
e
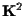 . .
DIMOSTRAZIONE
Sia 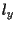 una retta incidente
una retta incidente 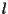 in
in 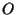 e sia
e sia 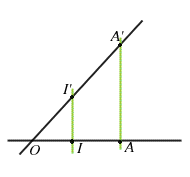 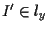 un punto arbitrario distinto da
un punto arbitrario distinto da 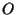 ;
se poniamo ;
se poniamo 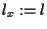 ,
allora sappiamo dal teorema precedente che i corpi ,
allora sappiamo dal teorema precedente che i corpi 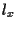 e
e 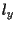 sono isomorfi e che ogni punto
sono isomorfi e che ogni punto 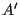 in
in 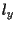 è immagine tramite l'isomorfismo esibito
è immagine tramite l'isomorfismo esibito 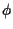 di un punto
di un punto 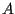 in
in 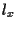 che si ottiene come illustrato in figura (in modo tale cioè che
che si ottiene come illustrato in figura (in modo tale cioè che
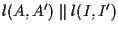 ). ).
 Sia
Sia
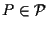 e siano
e siano 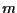 la retta passante per
la retta passante per 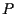 e parallela a
e parallela a 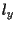 e
e 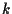 la retta passante per
la retta passante per 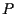 e parallela a
e parallela a 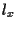 ;
sia ;
sia 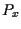 il punto di intersezione fra
il punto di intersezione fra 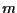 e
e 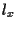 e sia
e sia
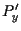 il punto di intersezione fra
il punto di intersezione fra 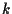 e
e 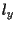 e consideriamo
e consideriamo 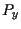 , la sua immagine inversa tramite , la sua immagine inversa tramite 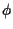 su
su 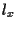 . .
L'associazione
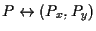 chiaramente istituisce una corrispondenza biunivoca che fa al caso nostro e si dice che le coordinate di
chiaramente istituisce una corrispondenza biunivoca che fa al caso nostro e si dice che le coordinate di 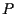 , rispetto agli assi fissati, sono , rispetto agli assi fissati, sono
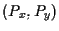 . .
Nel seguito eviteremo la notazione, peraltro diffusa,
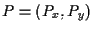 ma diremo semplicemente che
ma diremo semplicemente che 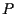 ha coordinate
ha coordinate 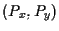 . .
Si osservi che se 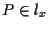 allora
allora 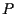 ha coordinate
ha coordinate 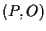 ,
mentre se ,
mentre se 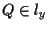 allora
allora 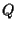 ha coordinate
ha coordinate 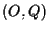 e in particolare
e in particolare 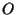 ha coordinate
ha coordinate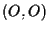 , ,
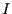 ha coordinate
ha coordinate 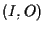 e
e 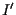 ha coordinate
ha coordinate 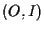 . .
|













 Sia
Sia
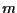 e
e 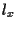 e sia
e sia

 _______________
_______________
 __
__
 ________________________
________________________



 Sia
Sia
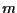 e
e 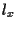 e sia
e sia

 _______________
_______________
 __
__
 ________________________
________________________