

 |
 |
 |
 |
 |
 |
 |
 |

|

|
Ricordiamo che due anelli
![]() si dicono isomorfi se esiste un'applicazione biunivoca
si dicono isomorfi se esiste un'applicazione biunivoca
![]() tale che
tale che
![]() ,
,
![]() ,
,
![]() e
e
![]() .
.
Due corpi si dicono isomorfi se lo sono come anelli, identicamente due campi.
DIMOSTRAZIONE
CASO 1 Supponiamo
Dobbiamo trovare un isomorfismo
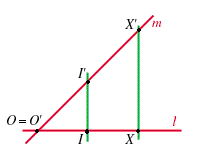
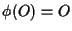
-
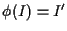
-
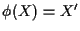 ove
ove 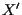 è il punto di intersezione di
è il punto di intersezione di 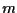 con la retta passante per
con la retta passante per 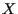 e parallela a
e parallela a 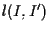 .
.
Poiché se ![]() allora
allora
![]() si ha che
si ha che ![]() è iniettiva e suriettiva.
è iniettiva e suriettiva.
Dobbiamo far vedere che ![]() conserva la moltiplicazione e l'addizione.
conserva la moltiplicazione e l'addizione.
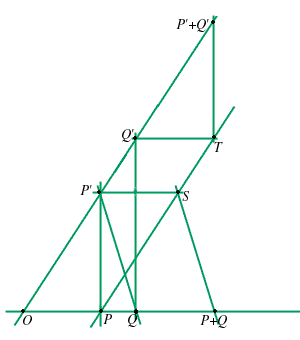
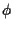 conserva l'addizione:
conserva l'addizione:
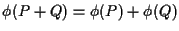

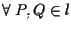
cioè con le nostre notazioni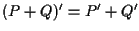 .
.
Calcoliamo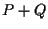 utilizzando
utilizzando  (e
(e  )
e calcoliamo
)
e calcoliamo 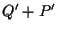 utilizzando
utilizzando 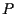 (e
(e 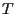 ); cosí operando otteniamo
); cosí operando otteniamo
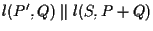 e
e
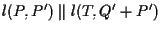 .
.
Utilizzando il Teorema di Desargues relativamente ai triangoli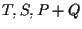 e
e 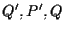 otteniamo che
otteniamo che
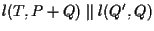 ; ma abbiamo che
; ma abbiamo che
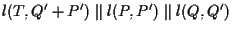 e questo implica che
e questo implica che 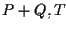 e
e 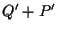 sono allineati lungo una retta parallela a
sono allineati lungo una retta parallela a 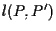 .
.
Siccome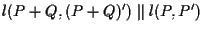 avremo proprio che
avremo proprio che
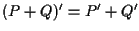 .
.

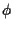 conserva la moltiplicazione:
conserva la moltiplicazione:
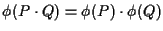

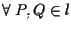
cioè con le nostre notazioni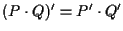 .
.
Per mostrare che conserva la moltiplicazione calcoliamo
conserva la moltiplicazione calcoliamo 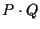 utilizzando
utilizzando 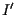 (e
(e 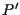 )
e calcoliamo
)
e calcoliamo
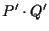 utilizzando
utilizzando 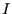 (e
(e 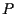 ); poi calcoliamo
); poi calcoliamo
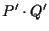 utilizzando
utilizzando 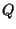 (e
(e 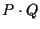 ); quindi
); quindi
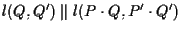 e dunque proprio
e dunque proprio
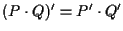 .
.
CASO 2
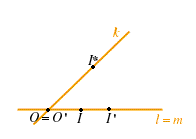 Supponiamo
Supponiamo Grazie a quanto ottenuto in CASO 1 otteniamo che
CASO 3
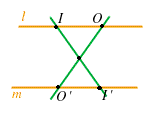 Supponiamo
Supponiamo
Senza ledere la generalità possiamo supporre che
Se
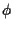 conserva l'addizione:
conserva l'addizione: 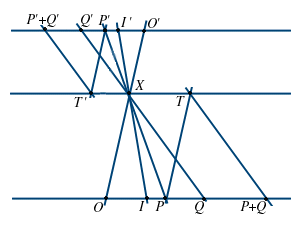 infatti, dati
infatti, dati  calcoliamo
calcoliamo 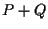 utilizzando
utilizzando 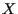 (e
(e 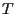 )
e calcoliamo
)
e calcoliamo 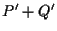 utilizzando
utilizzando 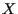 (e
(e 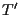 ).
).
Applicando il Teorema di Desargues B alle terne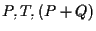 e
e
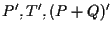 otteniamo che
otteniamo che 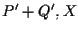 e
e 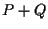 sono allineati e di qui
sono allineati e di qui
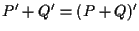 .
.
 conserva la moltiplicazione:
conserva la moltiplicazione: 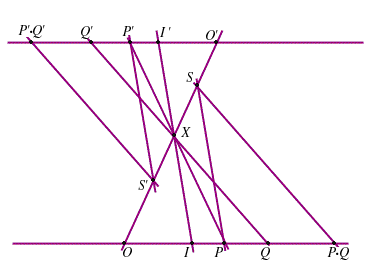 infatti moltiplichiamo
infatti moltiplichiamo 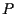 e
e 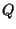 utilizzando
utilizzando 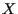 (e
(e 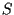 )
e moltiplichiamo
)
e moltiplichiamo 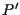 e
e 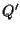 utilizzando
utilizzando 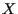 (e
(e 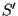 ).
).
Ancora una volta applicando il Teorema di Desargues B alle terne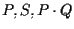 e
e
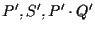 otteniamo che
otteniamo che
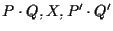 devono essere allineati e
quindi come prima
devono essere allineati e
quindi come prima
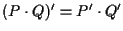 .
.
CASO 4
 Supponiamo
Supponiamo Sia
CASO 5
 Supponiamo
Supponiamo Da CASO 4 sappiamo che
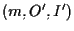 è isomorfo a
è isomorfo a In particolare se
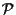 è pappiano otteniamo che i due campi
è pappiano otteniamo che i due campi 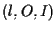 e
e 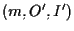 sono isomorfi.
sono isomorfi.

 _______________
_______________
 __
__
 ________________________
________________________