|
| Introduzione |
| Isometrie nello spazio |
| Solidi platonici |
| Simmetrie dei solidi platonici |
| Bibliografia |
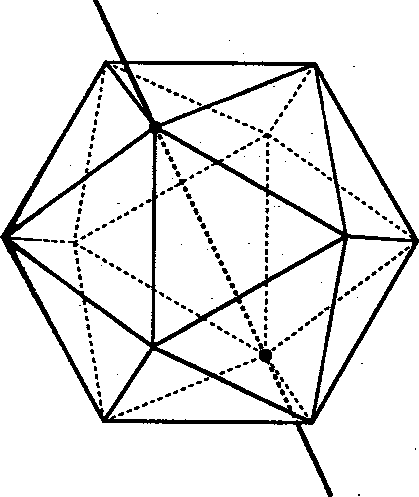
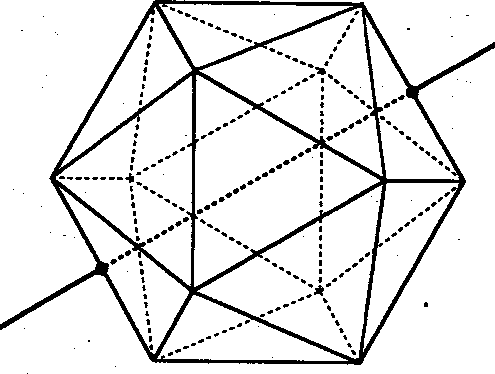
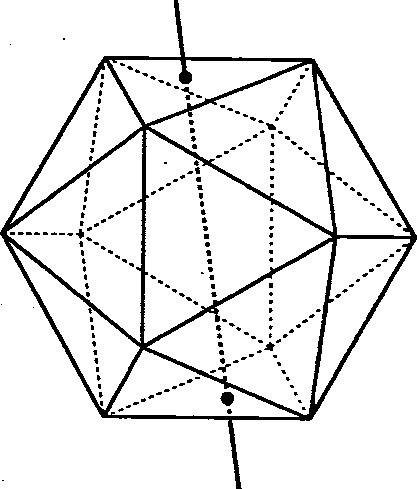
GRUPPO DI SIMMETRIA DELl'ICOSAEDRO
Studiamo le rotazioni diverse dall'identità dell'icosaedro I analogamente a quanto fatto per il cubo:
| Rotazioni | ||
|
||
|
||
|
||
| Il gruppo ha 60 rotazioni inclusa l'identità | ||
| Riflessioni e Riflessioni rotatorie | ||
| Si dimostra inoltre che le riflessioni e riflessioni rotatorie sono 60. | ||
| Quindi il gruppo di simmetrie dell'icosaedro, così come quello del dodecaedro, ha 120 elementi, cioè | ||
|Γ(I)| = 120 |
 |