Determinare il carattere della serie applicando il criterio più appropriato
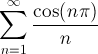
La serie data è a termini alterni (vedi esercizio precedente).
Potremmo applicare il criterio del confronto alla serie dei moduli e se riuscissimo in questo modo a provare la convergenza della serie, per il risultato visto nella sezione "Teoria" avremmo che tale serie converge assolutamente e dunque anche semplicemente.
D'altra parte
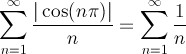
che sappiamo non essere convergente.
Ne concludiamo che la serie data non converge assolutamente ma questo non implica che non debba convergere semplicemente.
Applichiamo infatti il criterio di Leibnitz:
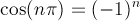
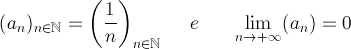
Ergo, per il criterio di Leibnitz, la serie data è convergente.
