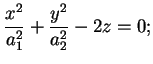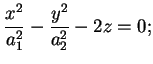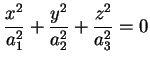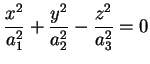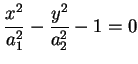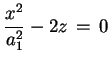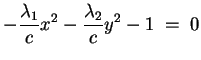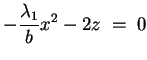Dimostrazione del Teorema 3
Sia
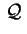 una quadrica d'equazione
(1.1).
Mostriamo che una quadrica d'equazione
(1.1).
Mostriamo che
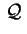 è riducibile ad una delle è riducibile ad una delle 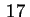 equazioni dell'enunciato.
Sia equazioni dell'enunciato.
Sia
 una quadrica non degenere a centro
( una quadrica non degenere a centro
(
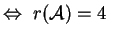 e e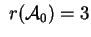 ); possiamo considerare la sua equazione
della forma
dove ); possiamo considerare la sua equazione
della forma
dove
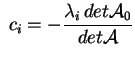 e e
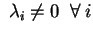 . .
Analizziamo le varie possibilità per i segni delle 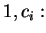
Affinchè siano tutti positivi occorre che
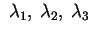 abbiano lo stesso segno,
che sarà anche il segno di abbiano lo stesso segno,
che sarà anche il segno di
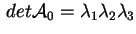 . Di conseguenza i prodotti . Di conseguenza i prodotti
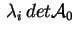 saranno positivi,
indipendentemente dal segno dei saranno positivi,
indipendentemente dal segno dei
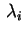 ,
quindi per essere ,
quindi per essere
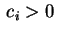 occorre che occorre che
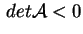 . .
Siamo allora nel caso in cui
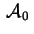 è definita
positiva o negativa e è definita
positiva o negativa e
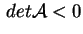 . Se poniamo . Se poniamo
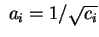 per per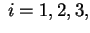 otteniamo
una superficie d'equazione
detta ellissoide reale. otteniamo
una superficie d'equazione
detta ellissoide reale.
Se due dei 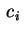 sono positivi e uno negativo, possiamo
assumere che sono positivi e uno negativo, possiamo
assumere che 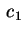 e e 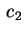 siano positivi e siano positivi e 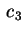 sia negativo. Abbiamo allora che
sia negativo. Abbiamo allora che
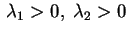 e e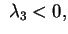 oppure oppure
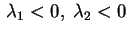 e e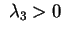 . Nel primo caso . Nel primo caso
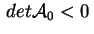 e quindi per avere e quindi per avere
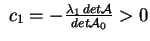 occorre che sia
occorre che sia
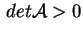 .
Analogamente nel secondo caso si avrà .
Analogamente nel secondo caso si avrà
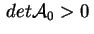 e e
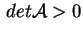 . .
Siamo nel caso in cui
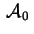 ha segnatura ha segnatura 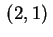 oppure oppure 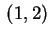 , e , e
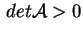 . Se
poniamo . Se
poniamo
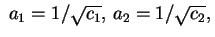 e e
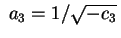 otteniamo una superficie d'equazione otteniamo una superficie d'equazione
detta iperboloide a una falda.
Il caso in cui un solo 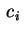 è positivo (ad esempio è positivo (ad esempio 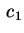 ) e gli altri due negativi è analogo al precedente.
Abbiamo, cioè, ) e gli altri due negativi è analogo al precedente.
Abbiamo, cioè,
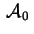 con segnatura con segnatura 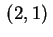 oppure oppure 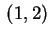 , e , e
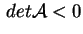 . Dopo
l'opportuna sostituzione l'equazione diventa
Questa quadrica si chiama iperboloide a due
falde. . Dopo
l'opportuna sostituzione l'equazione diventa
Questa quadrica si chiama iperboloide a due
falde.
L'ultimo caso si ha quando tutti i 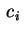 sono negativi.
Questo si avrà quando sono negativi.
Questo si avrà quando
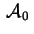 è definita
positiva o negativa e è definita
positiva o negativa e
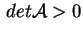 . Dopo l'opportuna
sostituzione l'equazione diventa
Questa quadrica si chiama ellissoide a punti non
reali. . Dopo l'opportuna
sostituzione l'equazione diventa
Questa quadrica si chiama ellissoide a punti non
reali.
Se
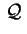 è una quadrica non degenere senza
centro, abbiamo visto che la sua equazione è del tipo
con è una quadrica non degenere senza
centro, abbiamo visto che la sua equazione è del tipo
con
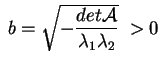 . Supponiamo di avere
gli autovalori . Supponiamo di avere
gli autovalori
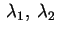 dello stesso
segno,ad esempio entrambi negativi (altrimenti cambiamo segno a
z). Effettuando la sostituzione dello stesso
segno,ad esempio entrambi negativi (altrimenti cambiamo segno a
z). Effettuando la sostituzione
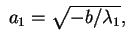
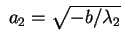 l'equazione diventa
questa quadrica si chiama paraboloide
ellittico. l'equazione diventa
questa quadrica si chiama paraboloide
ellittico.
Se gli autovalori hanno segno opposto,
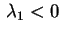 e e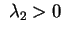 , effettuando la sostituzione , effettuando la sostituzione
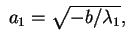
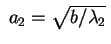 l'equazione diventa
questa quadrica si chiama paraboloide
iperbolico.
l'equazione diventa
questa quadrica si chiama paraboloide
iperbolico.
Esaminiamo ora le quadriche degeneri; Sia
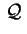 una
quadrica di rango 3; ci sono tre possibilità: il rango ridotto
di una
quadrica di rango 3; ci sono tre possibilità: il rango ridotto
di
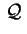 , o , o
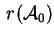 , può essere 3,
2 o 1.
Se , può essere 3,
2 o 1.
Se
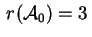 si tratta di una quadrica a
centro la cui equazione è del tipo
Supponiamo che gli autovalori siano dello stesso segno, ad
esempio tutti positivi; allora effettuando la sostituzione si tratta di una quadrica a
centro la cui equazione è del tipo
Supponiamo che gli autovalori siano dello stesso segno, ad
esempio tutti positivi; allora effettuando la sostituzione
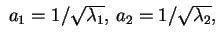 e e
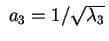 otteniamo l'equazione
che descrive un cono con un unico punto reale. otteniamo l'equazione
che descrive un cono con un unico punto reale.
Se gli autovalori sono uno positivo e due negativi oppure due
positivi e uno negativo allora effettuando la sostituzione
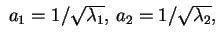 e e
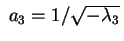 otteniamo l'equazione
che descrive un cono reale. otteniamo l'equazione
che descrive un cono reale.
Se invece
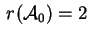 si tratta ancora di una
quadrica a centro la cui equazione è del tipo
con si tratta ancora di una
quadrica a centro la cui equazione è del tipo
con
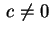 . Se si verifica il caso in cui i due autovalori
hanno stesso segno allora mediante una sostituzione opportuna
otteniamo una delle due equazioni
a seconda del segno del termine costante . Se si verifica il caso in cui i due autovalori
hanno stesso segno allora mediante una sostituzione opportuna
otteniamo una delle due equazioni
a seconda del segno del termine costante 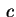 .Le equazioni
descrivono rispettivamente un cilindro ellittico
e un cilindro a punti non reali. .Le equazioni
descrivono rispettivamente un cilindro ellittico
e un cilindro a punti non reali.
Se gli autovalori hanno segno opposto si ottiene allora
che descrive un cilindro iperbolico.
Se infine
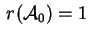 si tratta di una quadrica
senza centro la cui equazione è del tipo
con si tratta di una quadrica
senza centro la cui equazione è del tipo
con 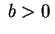 . Indipendentemente dal segno di . Indipendentemente dal segno di
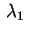 si ottiene, mediante la sostituzione
si ottiene, mediante la sostituzione
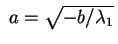 , l'equazione
che descrive un cilindro parabolico. , l'equazione
che descrive un cilindro parabolico.
Sia ora
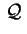 una quadrica di rango 2; si possono
avere i casi una quadrica di rango 2; si possono
avere i casi
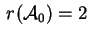 oppure 1. In entrambi i casi le quadriche hanno centro. oppure 1. In entrambi i casi le quadriche hanno centro.
Nel primo caso si ha un autovalore nullo; supponiamo si tratti di
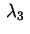 Ragionando come al solito rispetto al segno di Ragionando come al solito rispetto al segno di
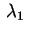 e e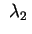 si hanno le equazioni
corrispondenti al caso in cui gli autovalori abbiano stesso segno
e quello in
cui i segni siano opposti. si hanno le equazioni
corrispondenti al caso in cui gli autovalori abbiano stesso segno
e quello in
cui i segni siano opposti.
Le equazioni descrivono, rispettivamente una
coppia di piani complessi coniugati incidenti e
una coppia di piani reali incidenti.
Nel secondo caso, cioè con
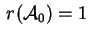 , si ha il
solo autovalore , si ha il
solo autovalore
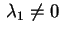 . Adoperando la solita
sostituzione otteniamo, a seconda del segno di . Adoperando la solita
sostituzione otteniamo, a seconda del segno di
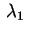 e di e di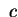 che descrivono, rispettivamente una coppia di
piani complessi coniugati distinti e paralleli e una
coppia di piani reali distinti e
paralleli.
che descrivono, rispettivamente una coppia di
piani complessi coniugati distinti e paralleli e una
coppia di piani reali distinti e
paralleli.
Concludiamo la trattazione col caso di una quadrica di rango 1.
Ovviamente anche il rango ridotto è 1
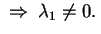 Tale quadrica ha equazione Tale quadrica ha equazione
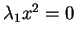 che ovviamente è congruente all'equazione
che descrive un piano doppio cioè il piano che ovviamente è congruente all'equazione
che descrive un piano doppio cioè il piano 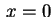 contato due volte. contato due volte.
|
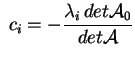 e
e
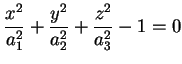
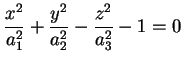
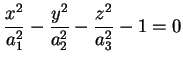
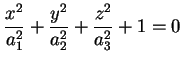
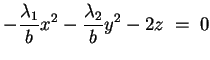
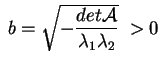 . Supponiamo di avere
gli autovalori
. Supponiamo di avere
gli autovalori