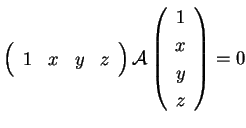Definizione     Def. generale Equivalenza affine Proprietà affini Quadriche a centro

Teoria delle quadriche

Definizione Sia $\,A^3(K)\,$ lo spazio affine associato allo spazio vettoriale $K^3$ e $E^3$ lo spazio 3-dimensionale euclideo. Una quadrica $\mathcal{Q}$ è rappresentata da un'equazione (detta equazione generale) della forma $$f(x,y,z) = a_{11}x^2+a_{22}y^2+a_{33}z^2+2a_{12}xy+2a_{13}xz+$$ $$+a_{23}yz+2a_{01}x+2a_{02}y+2a_{03}z+a_{00} \; = \; 0$$ (1.1)   nelle coordinate affini o cartesiane $x, y, z,$ dove $a_{ij}\in K$ e i coefficienti dei termini di secondo grado non sono simultaneamente nulli. Poniamo $a_{ij} = a_{ji}$ con $i,j = 0,1,2,3$ e $i > j$. La matrice simmetrica $$\mathcal{A} = \left( \begin{array}{cccc} a_{00} & a_{01} &... ... a_{30} & a_{31} & a_{32} & a_{33}\\ \end{array} \right)$$ è detta matrice della quadrica $[f]$.     ESEMPIO Osservazione   La matrice $\,\mathcal{A}\,$ è definita solo a meno di moltiplicazione per uno scalare non nullo, dato che la quadrica è definita da una classe di proporzionalità $[f]$. 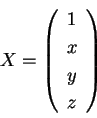Usando il simbolismo                  $$X = \left( \begin{array}{c} 1 \\ x \\ y \\ z\\ \end{array} \right)$$ l'equazione della quadrica assume la forma $$\left( \begin{array}{cccc} 1 & x & y & z\\ \end{array} \rig... ...al{A} \left( \begin{array}{c} 1 \\ x \\ y \\ z\\ \end{array} \right)=0$$ (1.2)   o equivalentemente      $\hspace{1cm} ^tX\mathcal{A}\hspace{1mm}X =0$. Denotiamo con 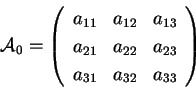$\,\mathcal{A}_0\,$ la seguente sottomatrice di $\,\mathcal{A}\,$: $$\mathcal{A}_0 = \left( \begin{array}{ccc} a_{11} & a_{12}... ..._{23}\\ a_{31} & a_{32} & a_{33}\\ \end{array} \right)$$ che rappresenta la forma quadratica $q$ di $f$. Abbiamo così dato una definizione di quadrica nello spazio 3-dimensionale. Esiste una definizione generale di quadrica come superficie nello spazio n-dimensionale.