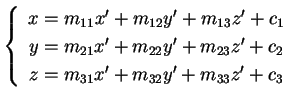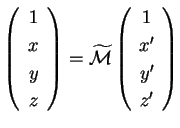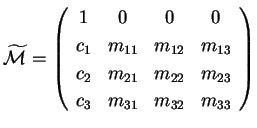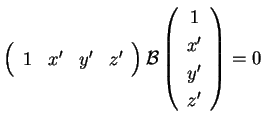|
Teoria delle quadriche |
|||||
Equivalenza affine
Definizione
Sia
L'affinità Consideriamo una matrice corrispondente all'affinità Ogni quadrica affinemente equivalente a 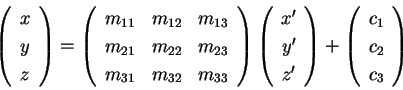
dove
Eseguendo la sostituzione (1.4) in (1.2) otteniamo l'equazione della quadrica dove è la nuova matrice della quadrica. Indichiamo con
Osservazione
Queste ultime considerazioni sono valide anche nel caso euclideo.
In
|
|