Teoria delle quadriche

Quadriche a centro

Considerando, ancora, il cambiamento del riferimento affine possiamo definire un'ulteriore caratteristica:

Definizione Una quadrica $\,\mathcal{Q} \,$ si dice a centro se esiste un riferimento affine $\,c,v_1,v_2,v_3 \,$ rispetto al quale $\,\mathcal{Q} \,$ non ha termini lineari. Ciò equivale a dire, se indichiamo con $\,\mathcal{B} = b_{ij}\,$ la matrice della quadrica nelle nuove coordinate, che $\,b_{i0} = 0 \,$ per ciascun $\,i = 1,2,3$ . L'origine $\,c\,$ di un tale sistema di riferimento si chiama centro della quadrica. Avremo, indicando con $\,g\,$ l'equazione della quadrica nelle nuove coordinate:

$\displaystyle g(x,y,z)$	$\displaystyle =$	$\displaystyle b_{11}(x)^2+b_{22}(y)^2+b_{33}(z)^2+2b_{12}xy+2b_{13}xz+b_{23}yz+b_{00}$
	$\displaystyle =$	$\displaystyle b_{11}(-x)^2+b_{22}(-y)^2+b_{33}(-z)^2+2b_{12}(-x)(-y)+ \cdots +b_{00}$
	$\displaystyle =$	$\displaystyle g(-x,-y,-z).$

Questo significa che il punto $\,c\,$ è un centro di simmetria per la quadrica $\,\mathcal{Q} \,$ .

Consideriamo la matrice 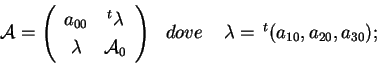$\mathcal{B}\: = \hspace{2mm} ^t\widetilde{\mathcal{M}} \hspace{1mm} \mathcal{A} \hspace{1mm} \widetilde{\mathcal{M}}\:$ e denotiamo:

$\begin{displaymath} \begin{array}{lcl} \mathcal{A} = \left( \begin{array}{cc}... ...e & \;\lambda = \,^t(a_{10},a_{20},a_{30});\\ \end{array} \end{displaymath}$

matrice della quadrica 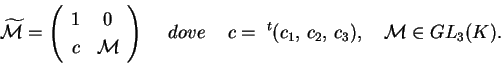$\,\mathcal{Q}$ .

$\begin{displaymath} \widetilde{\mathcal{M}} = \left( \begin{array}{cc} 1 & 0 ... ...m} c = \;^t(c_1,\,c_2,\,c_3), \quad \mathcal{M} \in GL_3(K). \end{displaymath}$

La matrice 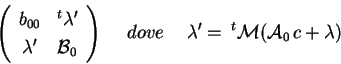$\,\mathcal{B} \,$ assumerà la forma:

$\begin{displaymath}\left( \begin{array}{cc} b_{00} & ^t\lambda' \\ \lambda'... ...{5mm}\lambda' = \:^t\mathcal{M}(\mathcal{A}_0\, c + \lambda) \end{displaymath}$

La condizione $\,b_{i0} = 0 \,$ per $\,i = 1,2,3 \,$ è equivalente a dire che:

$\displaystyle ^t\mathcal{M}(\mathcal{A}_0\, c + \lambda) = \lambda' = 0$

e siccome $\:\mathcal{M}$ , e quindi anche $\:^t\mathcal{M}$ , è invertibile la precedente equivale a:

$\displaystyle \mathcal{A}_0\, c + \lambda = 0.$

Tale sistema ha un'unica soluzione $\:c \in A^3(K)\:$ , che sarà il centro della quadrica, quando $\:\mathcal{A}_0 \,$ è invertibile. Abbiamo allora i seguenti risultati: PROPOSIZIONI 1, 2, 3.