|
Teoria delle quadriche |
||||||
|
Proposizione 1.
Diremo che la quadrica
Se il rango di
Proposizione 2.
Data una quadrica a centro
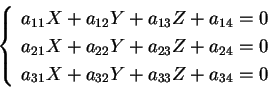
Esiste una relazione importante tra il rango di
Proposizione 3.
Sia
|
|
|
Teoria delle quadriche |
||||||
|
Proposizione 1.
Diremo che la quadrica
Se il rango di
Proposizione 2.
Data una quadrica a centro
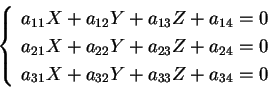
Esiste una relazione importante tra il rango di
Proposizione 3.
Sia
|
|