Teoria delle quadriche

Proprietà affini

Definizione 1 Le proprietà affini (o invarianti affini) sono proprietà che una superficie ha in comune con tutte quelle ad esse affinemente equivalenti.

Vediamo quali sono nel caso di una quadrica:
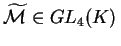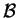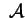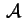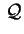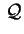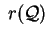poichè $\widetilde{\mathcal{M}} \in GL_4(K) \,$ dalla (1.7) si vede che $\mathcal{B} \;$ e $\; \mathcal{A}$ hanno lo stesso rango; quindi il rango di $\, \mathcal{A}$ è una proprietà affine della quadrica $\, \mathcal{Q}$ che chiameremo rango di $\, \mathcal{Q}$ e denoteremo con $\: r(\mathcal{Q})$ .
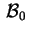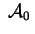Analogamente, dalla (1.8) si vede che anche $\,\mathcal{B}_0 \:$ e $\: \mathcal{A}_0 \,$ hanno la stesso rango.
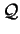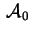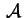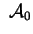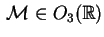Chiameremo rango ridotto di $\mathcal{Q}$ il rango della matrice $\,\mathcal{A}_0$ ; anche il rango ridotto è una proprietà affine. Nel caso reale sono proprietà affini anche il segno dei determinanti delle due matrici $\,\mathcal{A}\;$ e $\;\mathcal{A}_0$ . 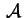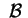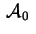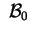Altre proprietà affini, molto importanti, si hanno quando il nuovo riferimento è ortonormale cioè quando $\,\mathcal{M}\in O_3(\mathbb {R})$ ; in questo caso $\,\mathcal{A}\;$ e $\;\mathcal{B} \;$ hanno lo stesso determinante, $\,\mathcal{A}_0 \;$ e $\;\mathcal{B}_0 \;$ sono matrici simili e hanno gli stessi autovalori, quindi la stessa segnatura.

Definizione 2 Diremo 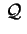$\, \mathcal{Q} \,$ non degenere o viceversa degenere a seconda che sia 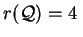$r(\mathcal{Q}) = 4 \:$ oppure 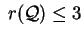$\: r(\mathcal{Q}) \leq 3$ . ESEMPIO