|
Teoria delle quadriche |
||||||
Osservazione
Per ogni
Infatti se prendiamo 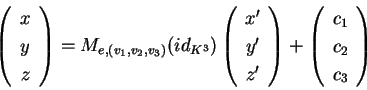
La precedente osservazione ci fa capire che data l'equazione |
|
|
Teoria delle quadriche |
||||||
Osservazione
Per ogni
Infatti se prendiamo 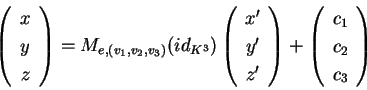
La precedente osservazione ci fa capire che data l'equazione |
|