Definizione     Def. generale Equivalenza affine Proprietà affini Quadriche a centro

Teoria delle quadriche

Definizione generale Consideriamo il campo $K = \mathbb {R}, \mathbb {C}$ ( $\mathbb {R} \,$ campo reale, $\mathbb {C} \,$ campo complesso). Sia $K^n$ l'$n$-spazio numerico su $K$. Definizione 1   Una funzione polinomiale quadratica è una funzione ${f:K^n \rightarrow K}$ tale che esistono una forma quadratica $q:K^n \rightarrow K$,  una forma lineare $\ell:K^n\rightarrow K$ e una costante $c\in K$ con $$f(x)=q(x)+\ell(x)+c$$ Definizione 2   Una quadrica in $\,K^n\,$ è un sottoinsieme $\,\mathcal{Q}\,$ di $\,K^n\,$ del tipo $$\mathcal{Q} = \{ x\in K^n \hspace{1mm} \vert\hspace{1mm} f(x)=0 \}$$ dove $f$ è una funzione polinomiale quadratica. Esempio     per $n=3$ sia $f:K^3 \rightarrow K$ data da: $$f(x,y,z) = \underbrace{2x^2+3y^2+3z^2+2xy}_{\mbox{forma quadratica }} \underbrace{-4x+2y-2z}_{\mbox{forma lineare}} + 4$$ Allora   $\quad 2x^2+3y^2+3z^2+2xy-4x+2y-2z+4=0 \quad$   rappresenta una quadrica in $K^3$. Due funzioni polinomiali quadratiche 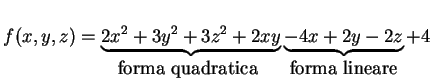$f$ e $g$ sono proporzionali quando esiste uno scalare $a \in K\backslash \{0\}$ tale che $g=af$. La relazione di proporzionalità tra funzioni polinomiali quadratiche è una relazione d'equivalenza. Quindi il sottoinsieme di $K^n$ definito dall'annullarsi di $f$ dipende solo dalla classe di proporzionalità di $f$ che d'ora in poi indicherò con $[f]$. Di solito una quadrica si indica con $\,\mathcal{Q}\,$ ma si intende che è data da una classe di proporzionalità $[f]$ tale che $f$ si annulla precisamente in $\,\mathcal{Q} \subseteq K^n$.