Classificazione Euclidea

Faremo ora una classificazione delle quadriche nello spazio euclideo $\,E^3 \,$ e daremo una rappresentazione grafica di quelle più importanti.

Teorema 1 Una quadrica $\,\mathcal{Q} \:$ di $\: E^3 \:$ è congruente ad una ed una sola delle seguenti (che sarà chiamata forma canonica di $\,( \mathcal{Q} \subset E^3)$ :

$\begin{displaymath} \begin{array}{ll} \displaystyle\frac{x^2}{a_1^2}+\displays... ...mbox{paraboloide iperbolico;}\\ \, & \, \\ \end{array} \end{displaymath}$

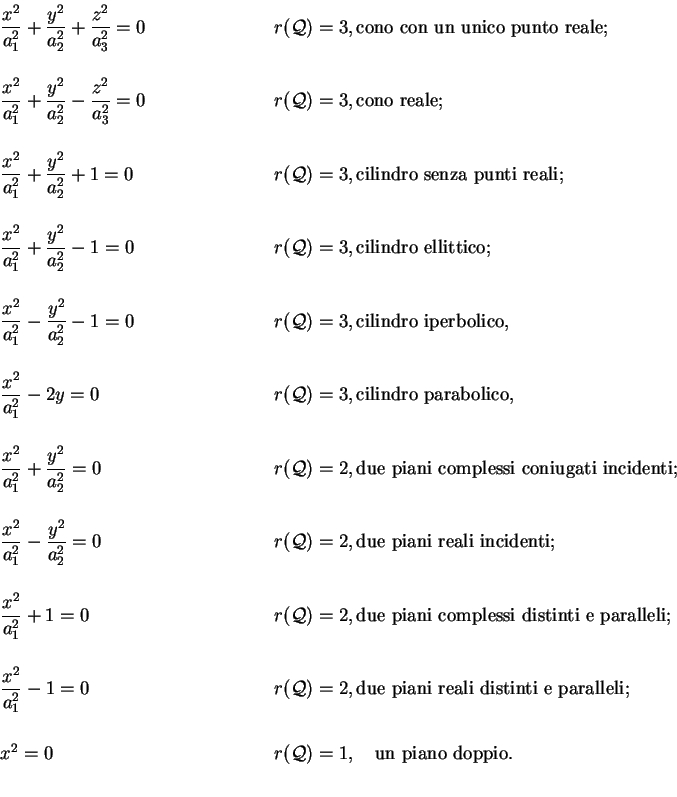
$\begin{displaymath} \begin{array}{ll} \displaystyle\frac{x^2}{a_1^2}+\displayst... ...\quad \mbox{un piano doppio.}\\ \, & \, \\ \end{array} \end{displaymath}$

Le quadriche precedenti sono a due a due non congruenti.

Alla dimostrazione del teorema premettiamo un'importante caratterizzazione dell'equazione di una quadrica non degenere in cui si tiene conto dei determinanti delle matrici $\,\mathcal{A} \;$ ed $\; \mathcal{A}_0 \,$ e della segnatura di $\,\mathcal{A}_0$ .
Caratterizzazione Dimostrazione del Teorema 3