Osservazione 1:
Il terzo passo della dimostrazione dei teoremi
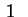
e
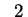
(normalizzazione dei coefficienti) non ha senso nel caso
euclideo, perchè le trasformazioni di coordinate adoperate non
sono ortogonali, e quindi le equazioni trovate non sono
ulteriormente riducibili.
Osservazione 2:
Dal teorema
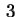
si può osservare che in
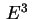
ci
sono infinite classi di congruenza di quadriche, contrariamente
al caso affine in cui le classi d'equivalenza
affine sono in numero finito.
Esse sono rappresentate dalle quadriche dell'enunciato al variare
dei parametri
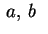
e
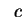
che vi compaiono.
Classificazione
