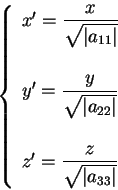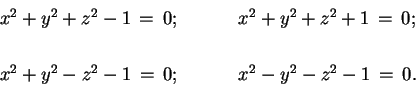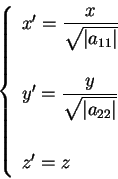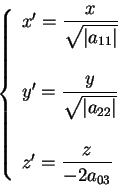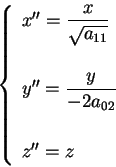Dimostrazione:
Sia
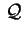 una quadrica d'equazione
(1.1).
Possiamo ripetere esattamente i primi due passi della
dimostrazione del teorema 1 ed ottenere quindi una
distinzione dei vari tipi di quadriche espressa dalle equazioni
(2.2),
(2.3),
(2.4),
(2.5) e
(2.6).
Ripartiamo dunque da:
Sia
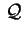 una quadrica a centro; È stata, dunque,
trasformata nella quadrica d'equazione
(2.2);
possiamo supporre che una quadrica a centro; È stata, dunque,
trasformata nella quadrica d'equazione
(2.2);
possiamo supporre che
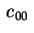 sia sia 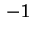 (se (se
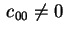 basta moltiplicare primo e secondo membro della
(2.2)
per basta moltiplicare primo e secondo membro della
(2.2)
per
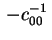 ) ed eseguire la trasformazione ) ed eseguire la trasformazione
con la quale ci si riconduce ad una delle seguenti forme (a
seconda dei segni dei coefficienti):
Se invece
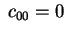 , utilizzando sempre la
trasformazione precedente, la quadrica , utilizzando sempre la
trasformazione precedente, la quadrica
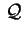 risulta essere affinemente equivalente a una delle due forme:
Abbiamo così ottenuto sei equazioni della lista. Le prime
quattro rappresentano i casi di quadriche non degeneri a
centro che sono: ellissoidi e iperboloidi; le altre due
rappresentano il caso di una quadrica degenere a centro
cioè il cono.
Sia ora
risulta essere affinemente equivalente a una delle due forme:
Abbiamo così ottenuto sei equazioni della lista. Le prime
quattro rappresentano i casi di quadriche non degeneri a
centro che sono: ellissoidi e iperboloidi; le altre due
rappresentano il caso di una quadrica degenere a centro
cioè il cono.
Sia ora
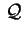 una quadrica non a centro. una quadrica non a centro.
Supponiamo sia stata trasformata nella quadrica d'equazione
(2.3);
possiamo supporre che sia
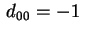 .
Mediante la trasformazione
otteniamo rispettivamente, al variare dei segni dei coefficienti,
le quadriche d'equazione .
Mediante la trasformazione
otteniamo rispettivamente, al variare dei segni dei coefficienti,
le quadriche d'equazione
Se invece
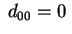 , utilizzando sempre la
trasformazione precedente, la quadrica , utilizzando sempre la
trasformazione precedente, la quadrica
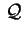 risulta essere affinemente equivalente a una delle due forme:
Se, invece,
risulta essere affinemente equivalente a una delle due forme:
Se, invece,
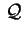 è stata trasformata nella
quadrica d'equazione (2.4),
eseguendo la trasformazione
otteniamo le quadriche d'equazione
Esse rappresentano il caso di quadrica non degenere, non a centro
(paraboloide).
Se è stata trasformata nella
quadrica d'equazione (2.4),
eseguendo la trasformazione
otteniamo le quadriche d'equazione
Esse rappresentano il caso di quadrica non degenere, non a centro
(paraboloide).
Se
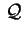 è stata trasformata nella quadrica
d'equazione (2.5) è immediato verificare che tale
superficie è affinemente equivalenete all'equazione è stata trasformata nella quadrica
d'equazione (2.5) è immediato verificare che tale
superficie è affinemente equivalenete all'equazione
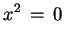 se 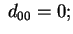
se abbiamo
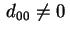 , supposto al solito , supposto al solito
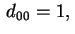 la quadrica è affinemente equivalente a una delle due
equazioni:
Se infine la quadrica è affinemente equivalente a una delle due
equazioni:
Se infine
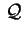 è stata trasformata nella quadrica
d'equazione (2.6) possiamo supporre è stata trasformata nella quadrica
d'equazione (2.6) possiamo supporre
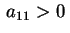 ed eseguendo la trasformazione
otteniamo la quadrica d'equazione
ed eseguendo la trasformazione
otteniamo la quadrica d'equazione
Abbiamo così esaurito tutti i possibili casi di
equazione di una quadrica in
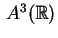 . Ognuna di esse
è affinemente equivalente ad una sola forma
canonica del teorema in quanto ogni quadrica della lista
differisce dalle altre per qualche invariante affine. . Ognuna di esse
è affinemente equivalente ad una sola forma
canonica del teorema in quanto ogni quadrica della lista
differisce dalle altre per qualche invariante affine.
|