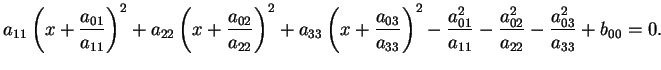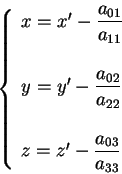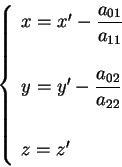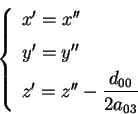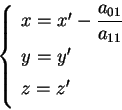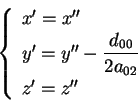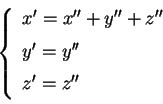Passo 2: eliminazione dei termini
di primo grado e del termine costante.
Supponiamo che
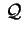 sia a centro. Applicando il
metodo del completamento dei quadrati alla
(2.1) otteniamo
Quindi attraverso la trasformazione affine (si tratta di una
traslazione)
l'equazione (2.1) si trasforma nella seguente: sia a centro. Applicando il
metodo del completamento dei quadrati alla
(2.1) otteniamo
Quindi attraverso la trasformazione affine (si tratta di una
traslazione)
l'equazione (2.1) si trasforma nella seguente:
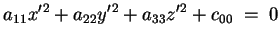 |
(2.2) |
dove
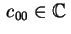 si ottiene in funzione dei
coefficiente della (2.1).
Sia si ottiene in funzione dei
coefficiente della (2.1).
Sia
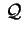 una quadrica non a centro e supponiamo,
salvo cambiare fra loro le variabili, che una quadrica non a centro e supponiamo,
salvo cambiare fra loro le variabili, che
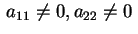 e e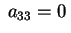 ,
la quadrica diagonalizzata sarà: ,
la quadrica diagonalizzata sarà:
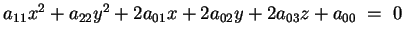 . .
Applicando il metodo del completamento dei quadrati e quindi la
trasformazione
otteniamo:
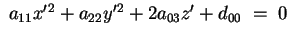 . .
Ora se
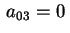 otteniamo l'equazione otteniamo l'equazione
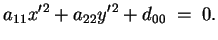 |
(2.3) |
Se invece
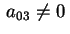 attraverso un'ulteriore
trasformazione del tipo:
l'equazione della quadrica diventa attraverso un'ulteriore
trasformazione del tipo:
l'equazione della quadrica diventa
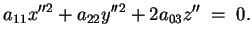 |
(2.4) |
Se supponiamo, invece,
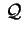 quadrica non a centro
e abbiamo, salvo cambiare fra loro le variabili, che quadrica non a centro
e abbiamo, salvo cambiare fra loro le variabili, che
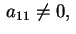 e e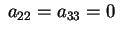 ,
la quadrica diagonalizzata sarà: ,
la quadrica diagonalizzata sarà:
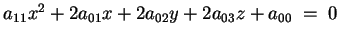 . .
Attraverso la trasformazione
vediamo che
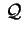 è affinemente aquivalente alla
quadrica
Consideriamo il caso in cui è affinemente aquivalente alla
quadrica
Consideriamo il caso in cui
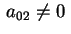 e e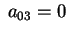 ; se si verificasse l'opposto, cioè ; se si verificasse l'opposto, cioè
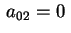 e e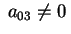 , scambiando tra loro gli
assi , scambiando tra loro gli
assi
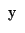 e e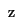 si ricadrebbe nel caso considerato. si ricadrebbe nel caso considerato.
Abbiamo, dunque, l'equazione
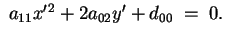
Ora se
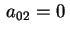 otteniamo la quadrica d'equazione otteniamo la quadrica d'equazione
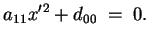 |
(2.5) |
Se, invece,
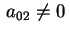 attraverso la trasformazione
Otteniamo la quadrica d'equazione attraverso la trasformazione
Otteniamo la quadrica d'equazione
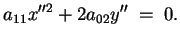 |
(2.6) |
Esaminando il caso in cui
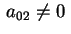 e e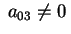 se consideriamo l'affinità
si ottiene un'equazione del tipo:
Possiamo ridurre tale equazione con i metodi visti nel
passo 1 e nel passo 2 ed ottenerne una del tipo:
Torniamo, dunque, in uno dei casi precedentemente trattati.
(Passo 3) se consideriamo l'affinità
si ottiene un'equazione del tipo:
Possiamo ridurre tale equazione con i metodi visti nel
passo 1 e nel passo 2 ed ottenerne una del tipo:
Torniamo, dunque, in uno dei casi precedentemente trattati.
(Passo 3)
|