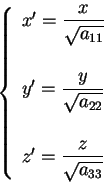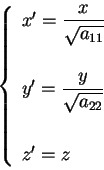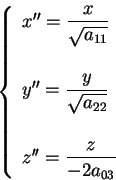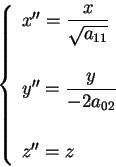Passo 3: normalizzazione dei
coefficienti.
Sia
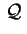 una quadrica a centro; È stata, dunque,
trasformata nella quadrica d'equazione
(2.2); possiamo
supporre che una quadrica a centro; È stata, dunque,
trasformata nella quadrica d'equazione
(2.2); possiamo
supporre che
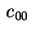 sia sia
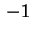 oppure oppure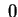 (se (se
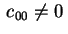 basta moltiplicare primo e secondo membro
della (2.2) per basta moltiplicare primo e secondo membro
della (2.2) per
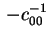 ).
Mediante la trasformazione
otteniamo rispettivamente le quadriche d'equazione ).
Mediante la trasformazione
otteniamo rispettivamente le quadriche d'equazione
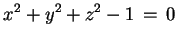 e 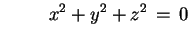
ossia prima e terza della lista del teorema. (Notare che
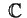 è algebricamente chiuso, quindi è algebricamente chiuso, quindi
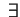 sempre sempre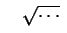 ) )
Sia ora
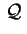 una quadrica non a centro. una quadrica non a centro.
Supponiamo sia stata trasformata nella quadrica d'equazione
(2.3); possiamo supporre che
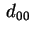 sia sia
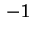 oppure oppure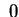 .
Mediante la trasformazione
otteniamo rispettivamente le quadriche d'equazione .
Mediante la trasformazione
otteniamo rispettivamente le quadriche d'equazione
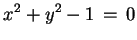 e 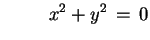
ossia la quarta e la sesta della lista del teorema.
Se, invece,
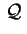 è stata trasformata nella
quadrica d'equazione (2.4);
eseguendo la trasformazione
otteniamo la quadrica d'equazione
ossia la seconda della lista del teorema. è stata trasformata nella
quadrica d'equazione (2.4);
eseguendo la trasformazione
otteniamo la quadrica d'equazione
ossia la seconda della lista del teorema.
Se
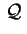 è stata trasformata nella quadrica
d'equazione (2.5) è immediato verificare che tale
superficie è affinemente equivalente all'equazione
cioè, le ultime due equazioni della lista del teorema. è stata trasformata nella quadrica
d'equazione (2.5) è immediato verificare che tale
superficie è affinemente equivalente all'equazione
cioè, le ultime due equazioni della lista del teorema.
Se infine
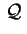 è stata trasformata nella quadrica
d'equazione (2.6) eseguendo la trasformazione
otteniamo la quadrica d'equazione
ossia la quinta della lista del teorema. è stata trasformata nella quadrica
d'equazione (2.6) eseguendo la trasformazione
otteniamo la quadrica d'equazione
ossia la quinta della lista del teorema.
Abbiamo così esaurito tutti i possibili casi di
equazione di una quadrica in
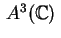 e ognuna di
esse è affinemente equivalente ad una sola
forma canonica del teorema. e ognuna di
esse è affinemente equivalente ad una sola
forma canonica del teorema.
|