L'insieme
Dimostrazione
Si ha
![]() .
.
![]() è un
sottogruppo di
è un
sottogruppo di ![]() infatti
infatti ![]() ,
e inoltre:
,
e inoltre:
- se
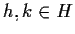 ,
allora
,
allora
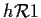 e
e
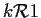 .
Essendo
.
Essendo
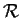 compatibile con il prodotto, si ha
compatibile con il prodotto, si ha
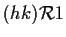 ,
cioè
,
cioè 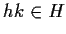 .
.
- se
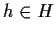 ,
,
![$[h] = [1] = [h]\cdot [h^{-1}]$](img13.gif) ,
cioè
,
cioè
![$[h^{-1}] = [1]$](img14.gif) .
Quindi
.
Quindi
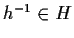 .
.
cioè
Dimostrazione
Si ha
![]() .
.
![]() è un
sottogruppo di
è un
sottogruppo di ![]() infatti
infatti ![]() ,
e inoltre:
,
e inoltre:
Dimostrazione
Se
![]() e
e
![]() ,
cioè se
,
cioè se
![]() e
e
![]() ,
si ha
,
si ha
![]() ;
da questo, per osservazione 5 della sezione "Sottogruppi normali", segue che
;
da questo, per osservazione 5 della sezione "Sottogruppi normali", segue che
![]() ,
cioè
,
cioè
![]() .
.